Seja , onde . Calcule , onde é a normal unitária exterior a nos seguintes casos:
é a esfera de raio com centro na origem;
Passo 1
Eaew, belezinha?
Precisamos calcular a integral de superfície
em que o campo vetorial é dado por
onde . Temos que a nossa superfície vai ser a esfera
Para este caso vamos usar a definição de uma integral de fluxo, ou seja, vamos calcular
Bora lá!
Passo 2
Primeiro precisamos de uma parametrização para a superfície esférica de raio , podemos usar coordenadas esféricas para obter
Se fizermos as derivadas parciais em rela��ão a e , temos que
e da mesma forma
Precisamos calcular o produto vetorial entre ambos os vetores, temos pela definição que
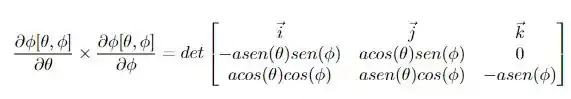
aplicando o determinante obtemos que
ou simplesmente
Note que podemos escrever este vetor normal como
Ou seja, como no primeiro quadrante , temos que o vetor normal está apontando para dentro da esfera, desta forma, o que precisamos realmente considerar
Precisamos usar isso em nossa integral! Vamos lá!
Passo 3
Temos a integral na forma
expandindo o produto escalar, obtemos
Usando a identidade trigonométrica, podemos obter que
Precisamos agora resolver as integrais! A integral em é bastante direta, portanto podemos escrever que
Agora vamos resolver as integrais em que estão faltando! Saca só!
Passo 4
Primeiro, podemos escrever que
lembrando da identidade trigonométrica, essa relação se torna
A primeira integral é conhecida como
e para a outra integral será conveniente utilizar a substituição simples
e
de forma que usando que e , podemos escrever
avaliando os limites de integração nos leva em
Ou seja, temos a seguinte integral
Vamos voltar para a nossa integral original agora!
A questão foi isso! Te vejo na próxima! Tchau Tchau!