Use o teorema do divergente para calcular o fluxo de
Através da superfície do sólido limitado pelo paraboloide e pelo plano .
Passo 1
Vamos começar fazendo um gráfico dessa região. Temos um paraboloide com simetria em virado para cima e o plano :
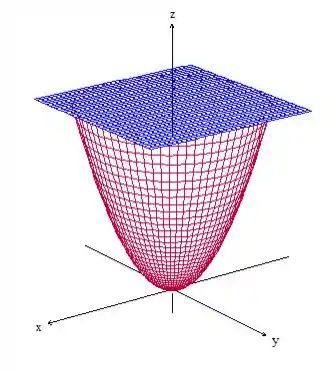
Como a região limitada por é fechada, sendo orientada positivamente, podemos aplicar o Teorema de Gauss:
Passo 2
Agora precisamos calcular . Temos:
Passo 3
Agora vamos montar a integral
Onde é o volume que vimos no passo 1.
Passo 4
Vamos agora, descrever essa região . Bom, escrever em coordenadas cartezianas vai dar um pouco de trabalho né. Como a região tem simetria em relação ao eixo e como temos termos quadráticos na integral, vamos usar coordenadas cilíndricas, você vai ver que a equação do paraboloide vai ficar bem simples nessas coordenadas.
Substituindo em , temos;
Certo. Agora, olhando para o desenho, vemos que a coordenada varia desde o paraboloide até o plano , portanto, .
Como temos uma volta completa no plano , .
O raio varia desde o eixo , onde até o seu máximo no topo da região, onde temos a circunferência no plano . Para descobrir esse valor máximo do raio, vamos, então, substituir na equação do paraboloide:
Como vemos, temos uma circunferência de raio lá em cima, portanto, .
Isso nos dá
Passo 5
Agora vamos resolver a integral: