UFMG, Sem Campus, Cálculo 3, P3 – 2023.1– Questão 3
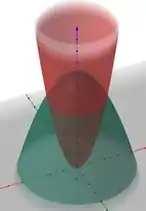
Dados os paraboloides e
- Faça um esboço do sólido limitado pelos paraboloides
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá.
Se a gente pegar o primeiro paraboloide, vamos ter
Vamos isolar o e passar para a esquerda dividindo:
Reparem que temos uma circunferência de raio . No caso, o valor de z vai representar a altura do paraboloide:
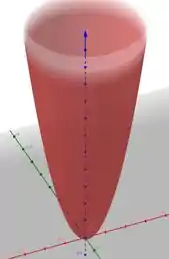
Passo 2
Agora vamos montar o do segundo parabolóide. Vamos ter
Aqui vamos fazer o mesmo processo do Passo 1:
Reparem que temos uma circunferência de raio . No caso, o valor de z vai representar a altura.
Lembrando que:
Com isso, o sólido limitado por ambos os paraboloides vai ser:
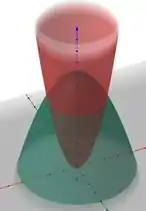
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 1-4, encontre a divergência do campo.4. O campo de velocidade da Figura 16.13.
Nos Exercícios 1-4, encontre a divergência do campo.
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = - y j ^ + z k ^ , e T o cilindro x 2 + y 2 ≤ 16 ,- 2 ≤ z ≤ 2
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = 2 i ^ + 2 j ^ = 2 k ^ e T a esfera x 2 + y 2 + z 2 ≤ 4
(Divergente em coordenadas polares) Seja Ω um campo aberto no semiplano y0 e seja F → x , y = P x , y i → + Q x , y j → , x , y ∈ Ω , com PeQ de classe C 1 . Seja P 1 θ ,ρ = P x , y e Q 1 θ ,ρ = Q x ,