Sejam e a fronteira do cilindro e .
Calcule , em que é o vetor normal unitário que aponte para fora do cilindro.
Passo 1
Antes de tudo, vamos ver melhor graficamente quem é essa superfície aí?
Ela é formada pelo cilindro de raio :
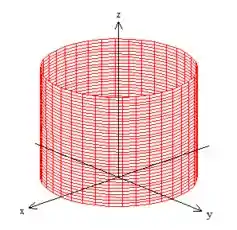
Mas calma! A superfície não tem apenas esse cilindro aberto!
Os planos e estão fechando o cilindro, e, portanto também fazem parte da superfície :
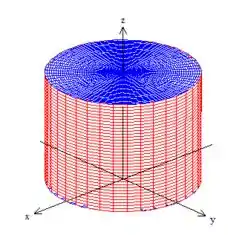
Esse sim é o nosso ! Uma superfície fechada delimitando um tronco de cilindro :D
Passo 2
Pow! Integral de superfície em cima de uma superfície fechada e com o vetor normal apontando para fora?! Cara, chama Gauss que ele resolve pra gente!:)
Hummm! Não sei não, heim! Ainda não me convenceu!
Então vou te convencer agora com o cálculo do divergente, veja só!
Passo 3
Pela teoria, a gente tem que
Onde esses caras aí, , , são as componentes do campo vetorial .
Como é dado por temos que
Calculando, portanto essas derivadas parciais, teremos
Percebeu? O divergente é easy! Então bora aplicar Gauss! :D
Passo 4
O teorema de Gauss nos fala o seguinte
Onde o é o sólido delimitado pela superfície fechada , ou seja, o tronco de cilindro. Além disso, ele deve estar com o vetor saindo... o que já temos, neh?!:)
Então basta calcular aquela integral tripla e o nosso problema terá se resolvido.
Passo 5
Substituindo o divergente na integral tripla...
Bem, para continuarmos as continhas devemos descrever a região :
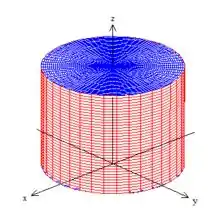
Como é um cilindro, uma substituição por coordenadas cilíndricas seria uma boa:
E o jacobiano da mudança é
Toda vez que realizamos uma troca de coordenadas, não podemos deixar de verificar os limites das novas variáveis, então me acompanha.
Passo 6
A primeira e mais imediata de todas é o , como o permaneceu inalterado, seu limite é o mesmo de antes, ou seja
Quanto ao ângulo , precisamos que ele dê uma volta completa, ou seja
O raio está limitado por e pelo raio máximo que é o raio do próprio cilindro:
Passo 7
Voltando para a integral tripla e dessa vez substituindo tudo
Trocando o jacobiano...
Calculando essa integral aí primeiro com relação à
Substituindo esse limite de integração em
Passando essa constante pra fora e agora integrando com relação a
Limites...