UFSC – Pré Cálculo – Lista 2 – Questão 4d
Dizer se é verdadeira ou falsa cada uma das sentenças abaixo:
Passo 1
E aí pessoal, tudo bem? O problema nos deu essa afirmação aqui
E pediu para verificar se ela é falta ou verdadeira
Esse é o símbolo de contido: significa que antes e depois dele vem conjuntos
É quando queremos indicar se algum subconjunto (parte de um conjunto maior) está dentro do outro conjunto. Também temos o elemento de negação desse sentido: o não contido . Esse símbolo nos afirma que tal subconjunto não pertence ao conjunto citado posteriormente.
Tudo bem até aqui? E aquele símbolo em que temos um conjunto menos o outro?
O que será que significa? Significa que os elementos que são de nosso interesse são todos elementos dos conjunto dos reais , menos os elementos dos racionais . Ou seja, precisamos relembrar quais são os elementos representativos desses conjuntos e verificar qual é o conjunto que queremos
Mas relaxa, vou fazer passo a passo com você!
Passo 2
A afirmação diz que
Então precisamos verificar se o primeiro conjunto está contido dentro dos reais . Vamos relembrar quais são os elementos dos reais?
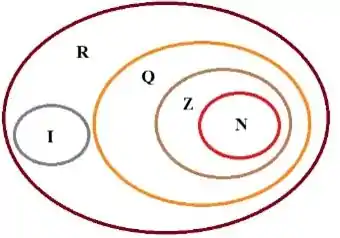
São todos os elementos dos conjuntos: naturais, inteiros, racionais e irracionais. Se retirarmos os elementos dos racionais , você percebe que na verdade estamos falando dos irracionais?
Pois é! Sendo assim, nossa afirmativa diz que o conjunto dos irracionais está contido no conjunto dos reais, e isso é verdade né?
Tranquilo até aqui?
Então a afirmativa é verdadeira
E é isso!
Espero ter ajudado! Vamos para a próxima?