Considere a função real f, dada pela lei
a) Desenhe o gráfico de
b) Calcule k, de modo que se tenha Se necessário, utilize a aproximação:
Passo 1
Primeiramente, vamos falar a respeito do domínio da nossa função, sabemos pela condição de existência que , Show?
Agora, vamos analisar a melhor a nossa lei de formação, observa ela um pouquinho:
Acho que você concorda comigo que a gente precisa mexer um pouco nela, rs. Afinal, está difícil entender o que faremos... A pergunta que não quer calar é: O que vamos fazer?
Lembra daquelas propriedades que a gente aplicava em logaritmos?
Observe a mágica acontecer:
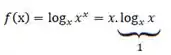
Portanto, o gráfico da função f, NESSE CASO, será o mesmo de uma função do 1º grau!!!

Nosso gráfico vai ficar assim:
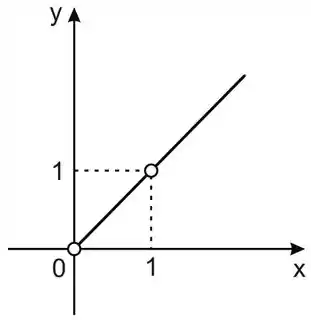
Muita atenção as restrições de domínio que vimos acima: . Por isso tanto no x igual a zero quanto no x igual a um, temos a “bolinha aberta”.
Shooow?
Passo 2
Agora vamos a parte b)
No item a) descobrimos que
Então, por consequência
Portanto, podemos escrever
Da seguinte forma:
Como queremos encontrar um valor que está no expoente, vamos aplicar um logaritmo de base 10 dos dois lados (Lembra? Logaritmo=Expoente).
Sendo que
Com isso temos:
O enunciado disse que, então:
Maneiro, né? =D
Resposta
a)
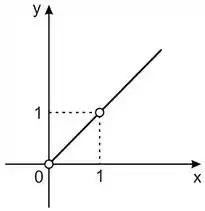
b)