A curva do gráfico abaixo representa a função
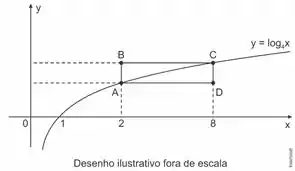
Qual a área do retângulo ABCD?
Passo 1
Beleza, sempre que você for resolver uma questão, algo importante é pensar o que você quer encontrar e qual a estratégia você vai usar para resolvê-la. No nosso caso, queremos encontrar a área do retângulo ABCD.
O que precisamos para encontrar a área?
No entanto, contudo, todavia... Para encontrarmos o valor da base e da altura necessitamos descobrir pelo menos as coordenadas de três dos 4 vértices.
Então essa é a primeira coisa que vamos fazer. Partiu?
Passo 2
Já sabemos que a base tem um tamanho 6, falta acharmos o tamanho da altura. Para isso, vamos descobrir a coordenada dos vértices C e A.
Vértice C
Vamos substituir o x na lei de formação para descobrirmos o valor de y. Nossa lei de formação é dada por:
Substituindo, ficamos assim:
Ou seja,
Vértice A
Vamos descobrir agora o , pois eles serão iguais. Vamos fazer isso porque caso tentássemos fazer igual fizemos acima, encontraríamos as mesmas coordenadas do vértice C. Vamos nessa:
Substituindo, ficamos assim:
Ou seja,
E o valor de é igual ao de . O nosso gráfico vai ficar assim, então:
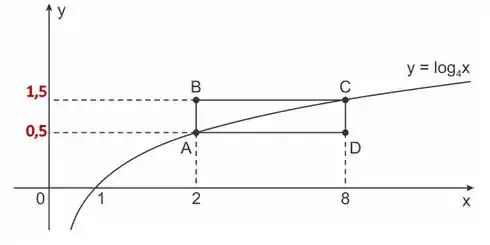
Ou seja, nossa altura será igual a
Passo 3
Nosso retângulo vai ficar com as seguintes dimensões:
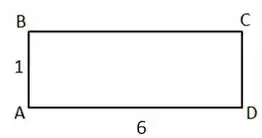
Agora é tranquilo calcularmos a área, vai ficar assim ó: