UFSC – Pré Cálculo – Exame – Questão 12
Qual é o domínio da função
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui!
O problema pediu para encontrar o domínio dessa função aqui
Mas calma! A ideia aqui é lembrar das condições de existência de um logaritmo!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Vamos supor que temos esse logaritmo aqui
Nós temos condições para que ele exista! são essas aqui
Então quando e são funções que dependem da mesma variável, como o por exemplo, eles PRECISAM satisfazer TODOS AO MESMO TEMPO as condições de existência!
beleza?
Passo 3
Agora vamos olhar nossa função de novo
Começando pela base , esse valor deve ser maior do que , então
Mas também deve ser diferente de :
Aí essas duas condições são para a base e ficam assim em uma reta numérica:
Agora vamos ver para o logaritmando . Ele deve ser positivo:
Essa é uma equação de segunda ordem, e aplicando a fórmula de bháskara para descobrir as raízes temos os valores e ! E como ela é uma parábola de bora pra cima podemos fazer um esboço dela
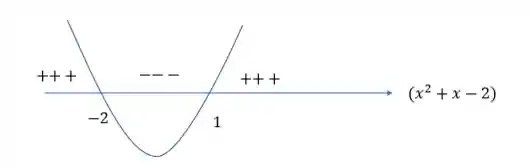
e agora? Agora vamos juntar todos esses intervalos e ver onde no domínio que as DUAS CONDIÇÕES são satisfeitas SIMULTANEAMENTE
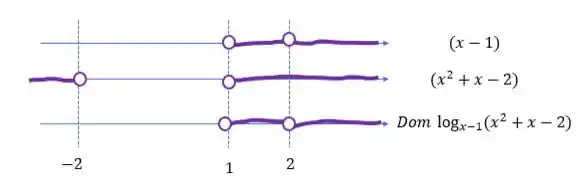
então o intervalo que ‘funciona’ para os dois ao mesmo tempo é o da terceira linha: entre 1 e 2 (sem incluir nenhum desses pontos, e ali a bolinha é aberta) e depois de 2:
A alternativa que diz isso é (A)
E é isso!
Espero ter ajudado! Vamos para a próxima?