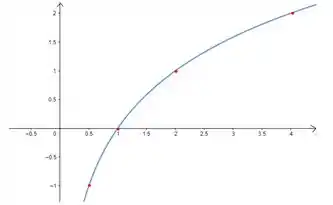
Esboce o gráfico da função abaixo
Passo 1
Vamos láá!! Queremos esboçar o gráfico da função
Certo?! Por onde podemos começar?

Primeira passo é verificar se a função será crescente ou decrescente! Como fazemos isso? Primeiro precisamos lembrar que uma função logarítmica tem a carinha
Onde é a base. Assim, se a base for maior que a função será crescente. Se a base for maior que zero e menor que a função será decrescente.
Beleza?!
Passo 2
Aqui a nossa base
Ou seja, a nossa função será crescente.

Passo 3
Agora para montar o esboço da função, podemos escolher alguns valores para para termos os valores de e montar o gráfico.
Para , teremos que
Como resolver esse logarítmo? Lembra que o logarítmo sempre está associado a um expoente?! Então, para resolver esse problema, vamos transformá-lo em um problema exponencial!!
Podemos fazer a seguinte pergunta para o logaritmo: “A base elevada a qual número tem como resultado ?”
O valor que satisfaz essa igualdade acima é o , certo?! Assim,
Podemos começar a montar nossa tabelinha:
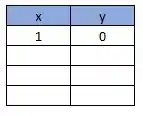
Para , teremos que
Utilizando o mesmo raciocínio anterior, a base elevada a 1 da o número . Ou seja,
Colocando esse valor na nossa tabela
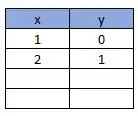
Para , teremos
Utilizando o mesmo raciocínio, chegamos ao valor
Incluindo esse valor na tabela, temos
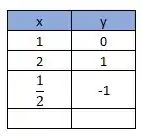
Pra finalizar, para
E assim,
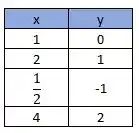
Passo 4
Com os valores que calculamos já conseguimos esboçar o gráfico da função .
Levando em consideração que a função será crescente e substituindo os valores da tabela
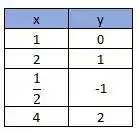
Teremos
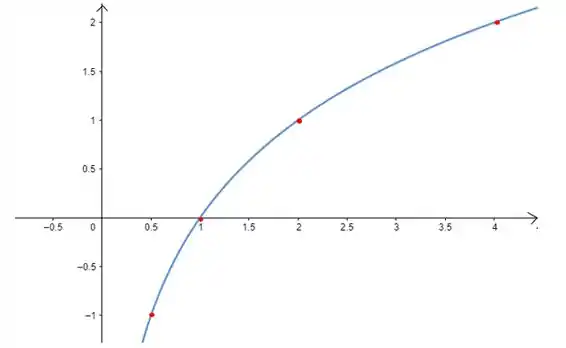
Beleza?!
Resposta