Listas de C2 - UFMG 2022.2 de Cálculo 2 da UFMG - 2ª Lista
Cálculo 2 - UFMG
A função pode ser escrita como série de potências com raio de convergência infinito. Ache a série de potências desta função em torno de 0.
Ver solução completaA função pode ser escrita como série de potências com raio de convergência infinito. Ache a série de potências desta função em torno de 0.
Ver solução completaA função
É representada por uma série de potências no intervalo . Ache essa série de potências.
Ver solução completaA função
É representada por uma série de potências no intervalo . Ache essa série de potências. Depois ache a série de potências que representa a função
Ver solução completaDefinimos as funções seno hiperbólico e cosseno hiperbólico por:
e
Calcule suas séries de Taylor em torno de .
Ver solução completaAche a equação em coordenadas polares para as curvas representadas pelas equações:
a)
Ver solução completaAche a equação em coordenadas polares para as curvas representadas pelas equações:
b)
Ver solução completaAche a equação em coordenadas polares para as curvas representadas pelas equações:
c)
Ver solução completaAche a equação em coordenadas polares para as curvas representadas pelas equações:
d)
Ver solução completaAche a equação em coordenadas polares para as curvas representadas pelas equações:
e)
Ver solução completaDiremos que um polinômio p(x) de ordem k é uma aproximação de ordem k de
uma função contínua f(x) para x “pequeno” se o limite
existe e é finito. Neste caso, diremos que f(x) ≃ p(x). No Exercício 6 foi visto que
. Use isto para mostrar que
Ver solução completaNa teoria da relatividade especial, a massa de um objeto se movendo com
velocidade é
onde é a massa do objeto em repouso e é a velocidade da luz. Neste caso a
energia cinética é dada por
Já a energia cinética na física clássica é calculada como
Use o Exercício 8 para mostrar que quando a velocidade é pequena
comparada com a velocidade da luz.
Ver solução completaEscreva uma curva parametrizada que passa por todos os pontos que satisfazem a equação:
Ver solução completaEscreva uma curva parametrizada que passa por todos os pontos que satisfazem a equação:
para .
Esboce a imagem desta curva. O que acontece com esta imagem quando o valor
de varia?
Ver solução completaSeja um número real positivo. Considere uma função derivável
tal que r para todo . Prove que
Ver solução completaSuponha que a função satisfaz para todo . Deste modo, podemos definir por:
Assuma que é derivável.
Mostre que
Ver solução completaUma curva parametrizada em coordenadas polares é uma curva
onde da forma
Note que
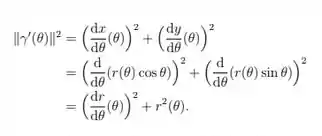
Assim o comprimento do arco da curva é dada pela equação:
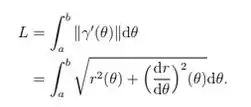
Usando isto, calcule o comprimento de arco quando da curva
Ver solução completaUma curva parametrizada em coordenadas polares é uma curva
onde da forma
Note que
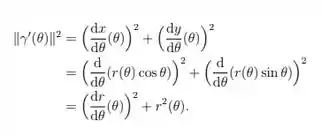
Assim o comprimento do arco da curva é dada pela equação:
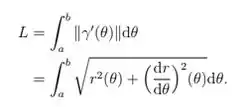
Usando isto, calcule o comprimento de arco quando da curva
Ver solução completaUma curva parametrizada em coordenadas polares é uma curva
onde da forma
Note que
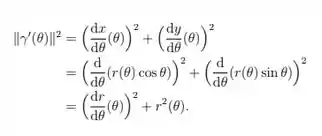
Assim o comprimento do arco da curva é dada pela equação:
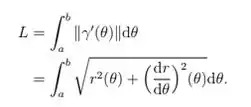
Usando isto, calcule o comprimento de arco quando da curva
Ver solução completaUma curva parametrizada em coordenadas polares é uma curva
onde da forma
Note que
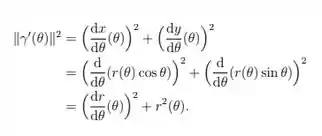
Assim o comprimento do arco da curva é dada pela equação:
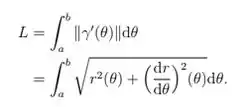
Usando isto, calcule o comprimento de arco quando da curva
Ver solução completa