Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Parametrizações Clássicas

Ver Teoria
Exercício 3712345678910111213141516171819202122232425262728293031323334353638394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889

Enunciado

UFMG, Sem Campus, Cálculo 2, Listas de C2 - UFMG 2022.2 - 2ª Lista, Questão 12

Escreva uma curva parametrizada γ   :   [ 0 ,   1 ]   →   R ² que passa por todos os pontos que satisfazem a ( x ,   y ) equação:

x ² / a ² + y ² / b ² =   1 ,

para a   >   0   e   b   >   0 .

Esboce a imagem desta curva. O que acontece com esta imagem quando o valor

de b varia?

Passo 1

Fala galera, tudo bem com vocês? Vamos para mais uma questão de Calc 2!!! Queremos encontrar uma parametrização para

x ² / a ² + y ² / b ² =   1 ,

Esboçar a imagem desta curva. E verificar o que acontece com esta imagem quando o valor

de b varia.

Vamos nessa!!!

Passo 2

Vamos encontrar uma parametrização para

x ² / a ² + y ² / b ² =   1 ,

Bem, essa é a nossa elipseee. Temos uma soma de coisas ao quadrado, então, vamos tentar escrever em função de seno e cosseno.

Vamos fazer

x = a c o s ( t )

y = b s i n ( t )

Fazendo isso, temos:

x ² / a �� + y ² / b ² =   1 ,

⇒ a ² c o s ² ( t ) / a ² + b ² s i n ² ( t ) / b ² =   1 ,

Logo

1 = 1

Ou seja, satisfazemos a equação. Logo, a parametrização é

( a c o s ( t ) , b s i n ( t ) )

Passo 3

Agora que temos a parametrização. Vamos desenhar a curva. Uma elipse é uma circunferência “achatada”. Como

x ² / a ² + y ² / b ² =   1 ,

Temos que para x = 0 ;     y = ± b e y = 0 ;     x = ± a . Logo, nosso gráfico fica

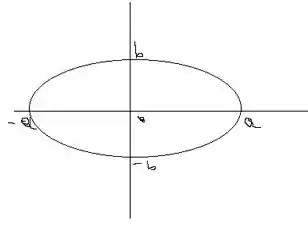
O que o termo b faz com nossa elipse. Pelo gráfico, se b for grande nossa elipse afina, e se for pequeno, ela achata.

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Desenvolvimento Acima

Exercícios de Livros Relacionados

Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.d) r → t = 2 cos 3 ⁡ t ,2 s e n 3 t , t ∈ 0 , π 2
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.b) r → t = t ,t + 2 ,4 - 2 t , t ∈ 0 ,1
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.a) r → t = 2 + 3 cos ⁡ t ,1 + 4 s e n t , t ∈ 0 ,2 π