UFMG, Sem Campus, Cálculo 2, Listas de C2 - UFMG 2022.2 - 2ª Lista, Questão 18a
Uma curva parametrizada em coordenadas polares é uma curva
onde da forma
Note que
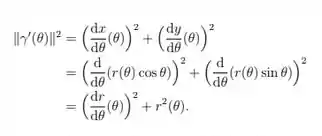
Assim o comprimento do arco da curva é dada pela equação:
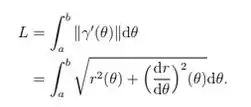
Usando isto, calcule o comprimento de arco quando da curva
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Calc 2!!! Queremos encontrar o comprimento de arco quando da curva
Para isso, vamo usar a fórmula
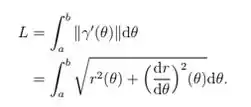
Vamos nessa!!!
Passo 2
Vamos começar calculando . Como a nossa curva é dada por
Temos que
Logo, o comprimento é dado por:
vamos começar fazendo nossas manipulações. Como . Então
Usando a identidade do arco metade , então
Integrando, temos
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Exercícios de Livros Relacionados
Uma curva, denominada bruxa de Maria Agnesi, consiste em todas as possíveis posições possíveis do ponto P na figura. Mostre que as equações paramétricas para essa curva podem ser escritas como x = 2 a
Deduza as Equações I para o caso π 2θπ .OBS:As equações I são as equações paramétricas do cicloide dadas por x = r ( θ - sen θ ) y = r ( 1 - cos θ ) θ ∈ R
Seja P um ponto a uma distância d do centro de um círculo de raio r . A curva traçada por P quando o círculo gira sobre uma reta é chamada trocoide. (Pense no movimento de um ponto sobre um raio de um
Identifique as simetrias das curvas nos Exercícios 1-12. Em seguida, esboce as curvas. r = 1 + cos θ
Identifique as simetrias das curvas nos Exercícios 1-12. Em seguida, esboce as curvas. r = 2 - 2 cos θ