UFMG, Sem Campus, Cálculo 2, Listas de C2 - UFMG 2022.2 - 2ª Lista, Questão 16e
Ache a equação em coordenadas polares para as curvas representadas pelas equações:
e)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para encontrar a equação em coordenadas polares para a seguinte curva:
Mas antes, vamos entender um pouquinho sobre as coordenadas polares.
Na coordenada polar, um ponto é representado por sua distância do ponto de origem () e pelo ângulo formado com o eixo positivo (), ou seja:
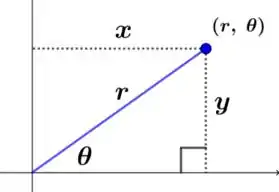
Assim, através da trigonometria, podemos observar as seguintes relações:
Dessa forma, basta aplicarmos essas relações na equação da curva que nos foi dada!!
E aí? Bora lá??!!
😉
Passo 2
Assim, substituindo e na equação , temos:
Pela identidade trigonométrica , temos:
Essa é a equação em coordenadas polares para a curva representada por .
Entendeu direitinho? Responde aee ;)
