USP, Sem Campus, Física 2, Provas Antigas, P2, 2022, 7
Uma corda de comprimento e densidade , com ambas as extremidades fixas, oscila no quarto harmônico de uma onda estacionária de acordo com a seguinte equação:
onde numa das extremidades da corda ( é dado em metros e em segundos).
Qual o comprimento da corda?
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma corda de comprimento que oscila no quarto harmônico de uma onda estacionária. Mas o que isso quer dizer?
Isso descreve omodo de vibração dessa onda estacionária, onde , repara só:
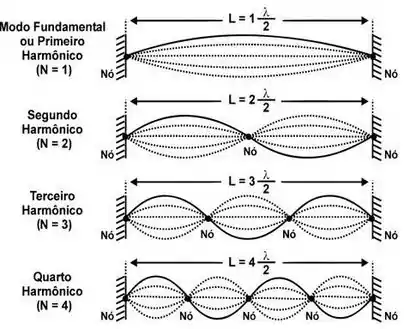
Cada modo de vibração tem equações diferentes para o cálculo do comprimento da corda , em função do comprimento de onda . No nosso caso,
Da forma geral dos modos de vibração, temos a equação de onda:
Comparando a equação da nossa onda:
temos e , certo? Mas pra calcular o valor de , nós precisamos do valor de . E nós podemos obter o valor de através de , é usar a equação:
Descobrindo esse valor, vamos obter o comprimento da corda através da equação .
Vamos lá!
Passo 2
Vamos começar calculando por meio da fórmula:
Da equação de onda que a questão nos deu, extraímos . Substituindo, temos:
Agora basta aplicar esse resultado na equação do comprimento:
Que é a nossa alternativa (A).
Prontinho, galera! Até a próxima! 😉