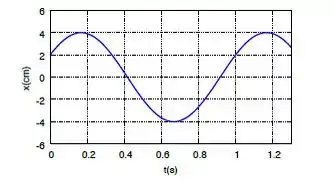
Observando o gráfico do MHS abaixo podemos dizer que é descrito pela função
Passo 1
Vamos analisar o gráfico para obter a informações relevantes a equação da onda. Do gráfico podemos ver que a amplitude está representada pelo eixo Y do gráfico é igual a , o período que representa o tempo necessário de uma crista a outra é igual a .
Portanto .
Então nossa equação fica:
Falta descobrir o ! Vamos pegar o ponto (1,2):
Então pode ser ou . Vamos pegar o ponto agora:
Nós não sabemos o valor de , mas sabemos pelo gráfico que ele tem que ser positivo.
Então tem que ser positivo, tem que estar no primeiro quadrante, então tem que ser negativo.
Portanto com essas informações podemos chegar a equação
Resposta
Letra b