Num movimento harmônico simples, a rapidez é máxima quando
(A) o módulo da aceleração é máximo.
(B) o módulo da aceleração é mínimo.
(C) o deslocamento é máximo.
(D) a energia potencial é máxima.
(E) a energia cinética é mínima.
Passo 1
Num movimento harmônico simples, a velocidade é máxima quando a aceleração está trocando de sentido. Ou seja, quando a aceleração é nula.
Passo 2
Se liga, nesse sistema massa-mola:
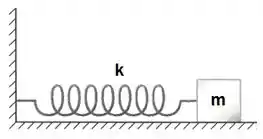
Quando a mola está esticada, a força elástica puxa o bloco:
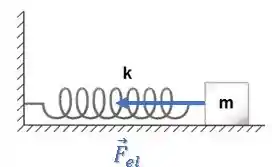
Então, ele está ganhando velocidade para a direita, enquanto a aceleração também é para a direita.
Passo 3
Conforme a mola vai ficando menos esticada, a força elástica vai diminuindo cada vez mais:
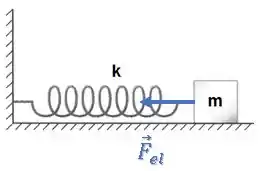
Porém o bloco ainda está ganhando velocidade, uma vez que a aceleração ainda é para a direita.
Essa situação vai ocorrer até que...
Passo 4
Até que a mola passe pela sua posição relaxada e a força elástica troque de sentido.
Quando a mola passar a ser comprimida, temos:
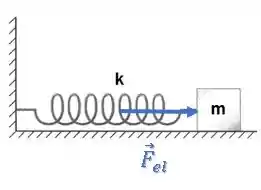
Ou seja, o bloco vai passar a diminuir sua velocidade, uma vez que a aceleração agora está contrária ao seu movimento.
Assim, a velocidade máxima do bloco ocorre exatamente nessa posição relaxada da mola, onde a aceleração é nula.
Ficamos com a letra (B).
Resposta
Letra (B)