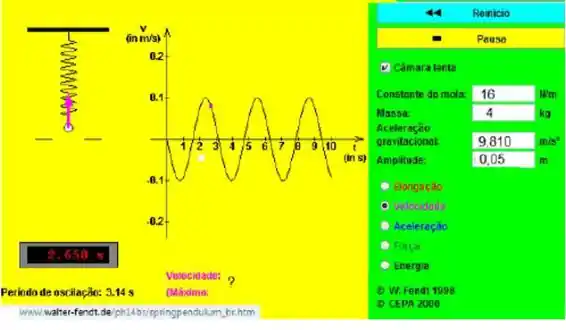
Um corpo de massa igual a 4kg foi preso à extremidade de uma mola, com k = 16N/m, a amplitude de oscilação foi igual a 0,05m. O conjunto oscilou durante um certo tempo (movimento harmônico simples), podemos afirmar que a velocidade máxima de oscilação foi igual a:
Passo 1
A velocidade máxima da onda é
Então precisamos descobrir quando a velocidade angular da onda para chegarmos a .
Logo
Resposta
Letra c
Exercícios de Livros Relacionados
A função x = 6,0m c o s [ ( 3 πr a d / s )t+ π / 3r a d ] descreve o movimento harmônico simples de um corpo. No instante t = 2,0s , qual é (a) o deslocamento, (b) a velocidade, (c) a aceleração e (
Duas partículas oscilam em movimento harmônico simples ao longo de um segmento retilíneo comum de comprimento A . As duas partículas têm um período de 1,5s , mas existe uma diferença de fase π / 6r a
Um objeto que executa um movimento harmônico simples leva 0,25s para se deslocar de um ponto de velocidade nula para o ponto seguinte do mesmo tipo. A distância entre esses pontos é 36c m . Calcule (a
Uma partícula executa um MHS linear com uma frequência de 0,25 H z em torno do ponto x = 0 . Em t = 0 , a partícula tem um deslocamento x = 0,37 c m e velocidade nula. Determine os seguintes parâmetro
13.10. Arrancada. A corda de um violão vibra com uma frequência igual a 440 Hz. Um ponto em seu centro se move com MHS com amplitude igual a 3,0 mm e um ângulo de fase igual a zero. a) Escreva uma equ