Uma corda é acionada por um gerador de ondas que estica a corda em uma direção perpendicular à corda, conforme apresentado na figura. A função de onda para a onda estacionária em uma corda, fixa em ambas as extremidades, é dada por , onde e estão em centímetros e está em segundos. Determine:
- O número de onda e o comprimento de onda das ondas da onda estacionária
- A frequência e a velocidade das ondas na corda
- O comprimento da corda, sabendo que a corda vibra em seu quarto harmônico
- Represente a onda estacionária, indicando a posição de cada nó. Considere a onda no instante e os extremos da corda em e
Passo 1
Oii galera, tudo certo? Bora lá? Essa questão aqui vai ser feitas aos poucos, letra por letra. Afinal, cada uma delas pede uma coisinha. A primeira coisa que podemos fazer, pra tudo ficar bem claro, é analisar a função dada:
Galera, unindo a matemática com a física, em uma função oscilatória qualquer (de seno ou cosseno), por exemplo:
Vamos ter os seguintes comportamento pro gráfico quando alteramos as constantes
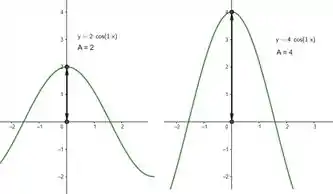
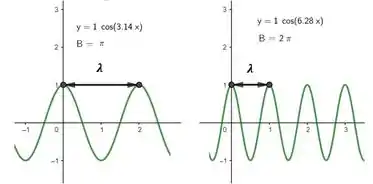
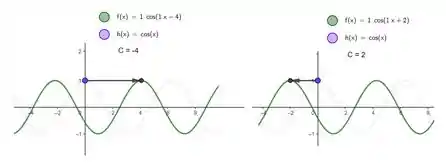
Sendo assim, vamos ter que:
- Amplitude de oscilação
- Seja o comprimento de onda, temos que , a exata definição de número de onda! Logo .
- Atraso de fase, se positivo. Adianto de fase, se negativo
Definido isso, já temos o suficiente pra responder a letra . Usando o do enunciado, vemos que:
Sendo assim, com as devidas unidades de medida do enunciado, temos que:
Passo 2
Pra responder a letra , vamos precisar olhar de novo pro nosso :
Se antes a gente olhou pra parte que envolvia a posição, vamos agora olhar pro pedaço que envolve o tempo! De forma análoga, seja:
Vamos ter, com variando:
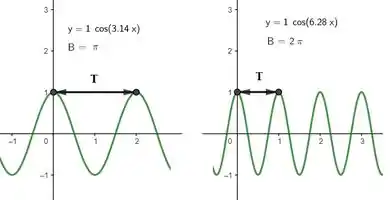
E logo:
E gente, essa é a definição de frequência angular! Logo, como:
Temos o suficiente pra responder a letra :
E a velocidade vai ser então:
Passo 3
Continuando então, vamos usar uma informação importante do enunciado: corda vibrando no quarto harmônico. Galera, quando isso acontece, a corda acaba assumindo o seguinte comprimento de onda:
O mesmo que:
Se a gente usar a fórmula:
Achamos a seguinte expressão pra frequência de oscilação
Ou seja, o comprimento que queremos saber será:
Substituindo:
Passo 4
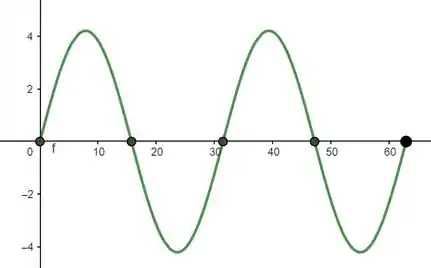
Pra gente fechar tudo tudinho, falta só a letra . Ela quer que a gente represente a onda estacionária:
Oras, isso nada mais é do que um esboço do gráfico! Para , como o enunciado pediu, temos:
Como cosseno de dá , o gráfico se reduz para:
Note ainda que, como , nas extremidades do domínio dessa função teremos:
Sendo assim, basta a gente esboçar uma função seno de de amplitude, que comece e termine em em seu domínio e que, como:
Caiba duas oscilações completas:
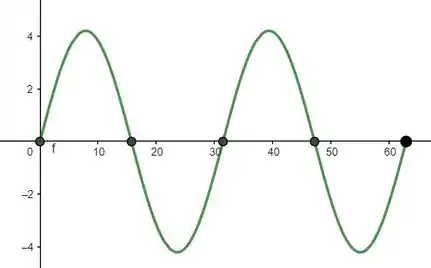
Ah e não esqueça de marcar os nós, ou seja, todos os pontos em que , como fizemos acima! Cabou!