UFSC – Cálculo 1 – Lista 1.10 – Questão C2c
Calcule os limites abaixo
Passo 1
Oi pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Bora lá?
O problema pediu para calcularmos esse limite aqui
Nosso instinto é logo substituir por , mas quando fazemos isso encontramos: , uma indeterminação!
Então a ideia é o seguinte: dividir esses polinômios por (já que é raiz dos dois), do polinômio resultante encontrar as outras raízes e fatorar por completo os dois, numerador e denominador
Com isso vamos conseguir simplificar ao máximo e avaliar novamente o limite!
Mas relaxa!
Vamos fazer passo a passo, juntinhos!
Passo 2
Nosso limite é
Vamos começar dividindo o numerador
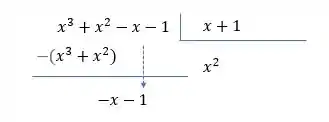
E terminando a divisão temos
Assim podemos escrever nosso polinômio como
E ainda podemos fatorar o resultado , aí nosso numerador fica completamente fatorado:
Beleza até aqui?
Passo 3
Passo 4
Passo 5
Passo 6
Passo 7
Agora vamos fatorar o denominador! Nosso limite
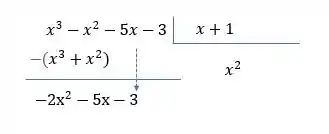
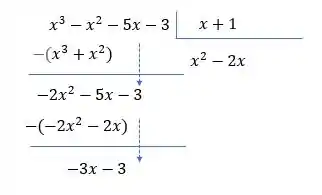E seguindo na divisão temos
Agora por fim o último passo dessa divisão:
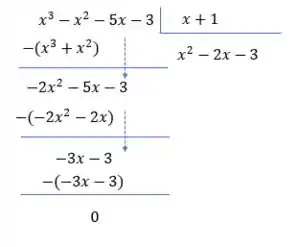Tudo bem até aqui? Podemos então reescrever nosso denominador
E para descobrir as outras duas raízes, vamos usar bascara:
Agora sim, conseguimos fatorar por completo nosso denominador
Ok?
vamos guardar esse resultado!
Passo 8
Agora vamos retornar ao nosso limite e substituir pelas formas fatoradas tanto do numerador quanto do denominador:
Do passo 2
Do passo 3:
Substituindo no nosso limite:
Viu só! Nosso limite ficou bem mais simples! Agora é só avaliar novamente o limite quando :
Beleza?
E taí nosso resultado!
Beleza?
Espero ter ajudado!