UFSC – Cálculo 1 – Lista 1.10 – Questão C2f
Calcule os limites abaixo
Passo 1
Oi pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Bora lá? Precisamos calcular esse limite aqui
Nosso instinto é substituir por e sair calculando, certo? Ok, então vamos lá:
Ué! Encontramos um denominador zero! Isso pode produção?
Mas qual é a diferença disso? É que quando o denominador se aproxima de zero, ou seja, é um número bem pequeno, o resultado dessa divisão é um número gigantesco!
Isso tem um nome na matemática: infinito!
Isso mesmo: quando o denominador de alguma fração tende à zero, em um limite por exemplo,
Agora nossa missão é saber se esse resultado é ou , e isso vamos descobrir analisando o sinal do limite!
Mas relaxa!
Vamos fazer passo a passo, juntinhos!
Passo 2
Nosso limite é esse aqui
O problema é embaixo, porque em cima quando o numerador vai mesmo para , já que a diferença entre eles é bem grande
Beleza?
Agora o denominador, em torno de temos uma raiz, ou seja, a função corta o eixo , então precisamos analisar o sinal que ele assume em torno de :
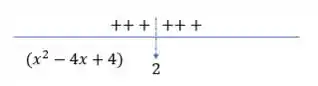
Pela briga dos sinais, temos que nosso limite vai à menos infinito!
E taí nosso resultado!
Beleza?
Espero ter ajudado!