UFRJ; Provas Antigas; Álgebra Linear; P2 2022.1; Questão 9
Seja
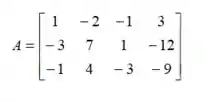
Se pertence ao núcleo de , então vale:
- -5
- -8
- -7
- -6
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de Algelin!!!
Nosso objetivo é descobrir a entrada do vetor . Sabemos que esse vetor pertence ao núcleo de , onde é a matriz.
Passo 2
Como pertence ao núcleo de , temos:
realizando o produto matriz vetor temos:
Juntando as duas equações acima temos:
Como temos uma igualdade entre vetores, então cada entrada tem que ser igual. Ou seja, temos que
Que é um sistema linear
Passo 3
No passo anterior conseguimos gerar o sistema
Vamos resolvê-lo! Vamos somar a primeira equação com a última. Então temos:
Achamos o valor de . Agora vamos substituir esse valor na primeira equação
E com isso chegamos a conclusão que
Prontinho, pessoal!! Finalizamos mais uma!!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊