Um barbante é enrolado ao redor de um círculo, e então desenrolado sendo mantido esticado. A curva formada pelo ponto , no final do barbante, é chamada de involuta do círculo. Suponha que o círculo tem raio e centro , e que a posição final de seja . Se o parâmetro for escolhido como na figura, encontre as equações paramétrias da involuta.
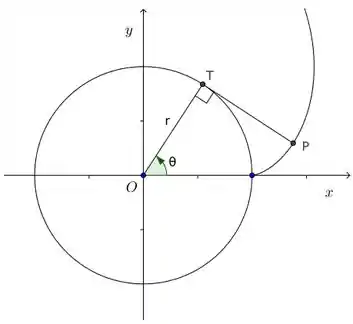
Passo 1
Para descobrirmos a parametrização da involuta, temos que achar o vetor posição do ponto .
Podemos pensar esse vetor como a soma dos vetores e
Veja na figura a seguir:
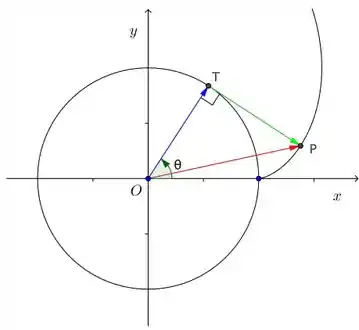
Passo 2
Sabemos que:
Pois o ponto pertence a circunferência, logo utilizamos a parametrização da circunferência para .
Perceba também que é igual ao comprimento do arco de circunferência localizado entre e o eixo , logo:
(comprimento do arco )
Passo 3
Beleza, agora podemos achar também um vetor tangente ao vetor :
Esse vetor é paralelo ao vetor , mas está no sentido oposto a ele. Vamos utilizar essas informações por partes.
Como está no sentido oposto de e , devemos inverter o sentido de :
(sentido invertido)
Como já sabemos que é paralelo a e a informação que temos sobre é a respeito de seu comprimento, vamos achar o comprimento de :
(porque
Opa, o comprimento de e diferem por um fator multiplicativo Então, para e virarem o mesmo vetor, temos que multiplicar por (para que os comprimentos dos dois vetores fiquem iguais, agora que eles já tem o mesmo sentido):
Passo 4
Agora, como sabemos que
Substituindo os resultados encontrados, temos:
,
Resposta
,