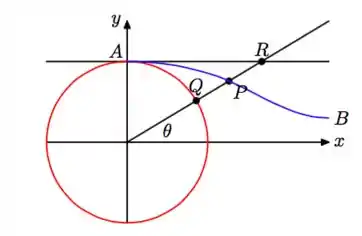
A reta que passa pela origem e faz ângulo com o eixo , intercepta a circunferência no ponto . Seja o ponto médio do segmento na figura abaixo. Determine as coordenadas de em função do ângulo . Perceba que, quando varia entre e , o ponto percorre a curva da figura.

Assim, tudo o que temos que fazer é encontrar cada uma dessas coordenadas! Comecemos pelo ponto ...

O que sabemos dele? Sabemos que pertence sempre à circunferência de raio ! Assim, podemos dizer que suas coordenadas estão no modelo:

Ok, e sobre o ponto , o que sabemos dele? Sabemos que sua coordenada é sempre constante e igual ao raio da circunferência! Assim,

E ainda podemos descobrir a relação que tem com e . Veja que no triângulo de vértices , e , temos que:

E, assim,

E o ponto pode ser descrito por:

Colocando esses valores para e na equação de , teremos:

Prontinho, aí está o nosso ponto !