Uma haste, presa na origem do plano , ocupa a posição da reta . A haste intercepta a reta no ponto e a elipse no ponto (figura). Quando varia, o vértice do triângulo descreve uma curva.
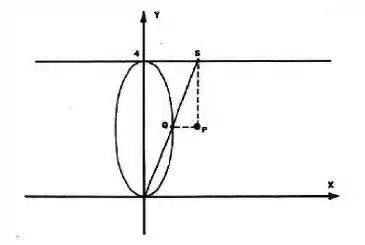
Escreva as equações paramétricas dessa curva em função do parâmetro .
Passo 1
Vamos lá, as coordenadas do ponto são:
O que a gente precisa é encontrar uma relação entre as coordenadas desse ponto e as coordenadas e dos pontos e .
Observando a figura a gente percebe que:
Assim
Passo 2
Agora vamos encontrar as coordenadas dos pontos e .
Comecemos pelo ponto .
O que sabemos dele? Sabemos que sua coordenada é sempre constante e igual ! Assim,
Agora, sabemos também que o ponto pertence à reta então:
Logo:
Passo 3
Para saber as coordenados do ponto , usamos o fato de que pertence a reta e a elipse . Assim, a coordenada do ponto é igual a :
Se substituirmos isso na equação da elipse, encontramos a coordenada do ponto Q
O caso não nos interessa pois representa a origem e nosso ponto não está na origem. Logo, as coordenadas do ponto Qsão:
Passo 4
Voltando agora para aquela relação que encontramos lá no incio.
Temos então que: