UFSC, Sem Campus, Cálculo C, Provas Professor Saeger - P2 2019.2, Questão 1
Parametrize a curva C definida por
E esboce duas de suas projeções nos planos coordenados.
Passo 1
Olá meu amigo, tudo na paz? Agora é a hora de resolver essa querida atividade. Primeira coisa é parametrizar a curva, e isso pode ser feito de várias formas.
Aqui, nós iremos chamar de e substituir nas equações.
Passo 2
Então,
Agora na segunda equação
Então nossa curva C pode ser dada por
Passo 3
Para esboçar as projeções de C nos planos coordenados, escolhemos duas coordenadas entre
E igualamos à variável do plano escolhido.
Escolhendo duas coordenadas de C pararem plotadas no gráfico, temos
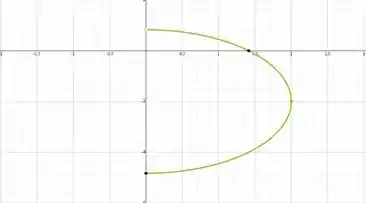
Então essa é a nossa projeção. Mas vale lembrar que essa é uma das possíveis projeções, pois podemos por exemplo parametrizar de outra forma nossa curva.
Resposta
Ver o desenvolvimento.
Exercícios de Livros Relacionados
Uma curva, denominada bruxa de Maria Agnesi, consiste em todas as possíveis posições possíveis do ponto P na figura. Mostre que as equações paramétricas para essa curva podem ser escritas como x = 2 a
Deduza as Equações I para o caso π 2θπ .OBS:As equações I são as equações paramétricas do cicloide dadas por x = r ( θ - sen θ ) y = r ( 1 - cos θ ) θ ∈ R
Seja P um ponto a uma distância d do centro de um círculo de raio r . A curva traçada por P quando o círculo gira sobre uma reta é chamada trocoide. (Pense no movimento de um ponto sobre um raio de um
Identifique as simetrias das curvas nos Exercícios 1-12. Em seguida, esboce as curvas. r = 1 + cos θ
Identifique as simetrias das curvas nos Exercícios 1-12. Em seguida, esboce as curvas. r = 2 - 2 cos θ