UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2, Questão 2
Esboce a trajetória das curvas espaciais abaixo.
Passo 1
Eaew, belezinha?
Temos que esboçar a trajetória das seguintes curvas espaciais:
Para isso temos que avaliar os valores de x, y e z para diferentes valores de t. Então vamos lá!
Passo 2
Vamos lembrar que uma curva parametrizada em termos de uma variável, possui o seguinte formato:
Sabendo disso, nós conseguimos identificar , e das curvas apresentadas no enunciado, e então avaliar os seus valores para diferentes valores de e assim esboçar o gráfico.
Passo 3
Olhando para a curva , temos que:
, e
Agora podemos construir uma tabela que contenha os valores de , e para diferentes valores de :
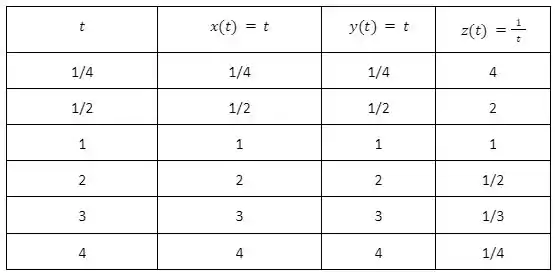
Com essas informações conseguimos esboçar o gráfico:
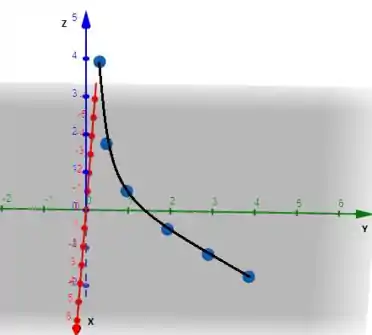
Passo 4
Olhando para a curva , temos que:
, e
Agora podemos construir uma tabela que contenha os valores de , e para diferentes valores de , como temos funções trigonométricas vamos escolher valores de que são frações de :
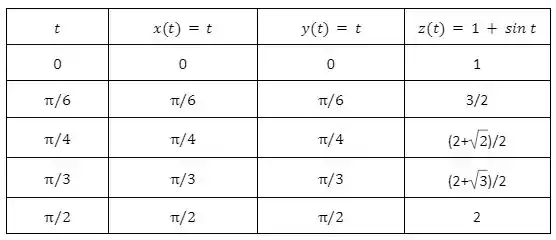
Com essas informações conseguimos esboçar o gráfico:
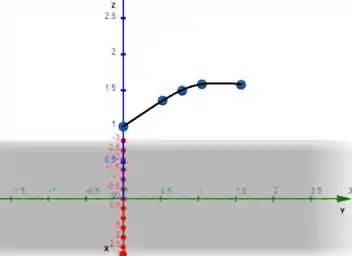
Passo 5
Olhando para a curva , temos que:
, e
Agora podemos construir uma tabela que contenha os valores de , e para diferentes valores de , como temos funções trigonométricas vamos escolher valores de que são frações de :
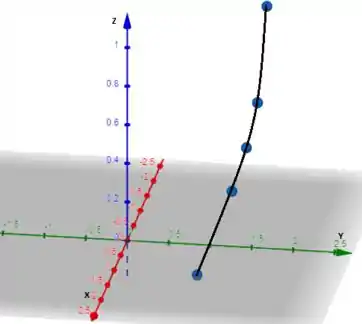
Com essas informações conseguimos esboçar o gráfico:
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
No decorrer da questão.