Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Parametrizações com Geometria

Ver Teoria
Exercício 18123456789101112131415161719202122232425262728293031323334353637383940

Enunciado

IME, 2020, VF, Q3A

Seja o campo vetorial F → x , y , z = ( 9 - x 2 + x 2 - y ,   y 2 - x + z ,   z + x - y ) . Seja a curva C como a interseção do cilindro x 2 + y 2 = 9 e o plano 2 x + 3 z = 6 , orientada no sentido horário.

  1. Represente a integral de linha do campo vetorial F → sobre a curva C através de uma integral simples definida.
  2. Determine o valor do campo vetorial F → sobre a curva C .

Passo 1

Fala, pessoal! Vejamos se esse truque ilumina o problema. Começando pelo cilindro, temos:

x = 3 cos ⁡ t                   y = 3 sin ⁡ t  

Aplicando na equação do plano, definimos z : 2 ⋅ 3 cos ⁡ t + 3 z = 6 ⇒ z = 2 - 2 cos ⁡ t

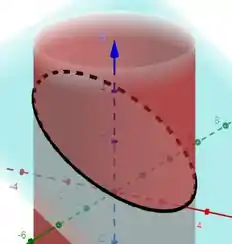
Assim a parametrização que pensei primeiro para C é:

σ t = ( 3 cos ⁡ t ,   3 sin ⁡ t ,   2 - 2 cos ⁡ t )

Porém, aqui está a pegadinha do Prof. do IME: essa parametrização é no sentido anti-horário e devemos invertê-la para atender o enunciado. Assim tome σ ( - t ) :

σ t : = 3 cos ⁡ t ,   - 3 sin ⁡ t ,   2 - 2 cos ⁡ t ,                     0 ≤ t ≤ 2 π

Passo 2

Agora, façamos:

∫ C F → ⋅ d   l → = ∫ 0 2 π F → σ ⋅ σ ' t   d t =

= ∫ 0 2 π ( 9 - 9 cos 2 ⁡ t + 9 cos 2 ⁡ t + 3 sin ⁡ t , 9 sin 2 ⁡ t - 3 cos ⁡ t + 2 - 2 cos ⁡ t ,   2 - 2 cos ⁡ t + 3 cos ⁡ t + 3 sin ⁡ t ) ⋅ ( - 3 sin ⁡ t ,   - 3 cos ⁡ t ,   2 sin ⁡ t )   d t =

= ∫ 0 2 π ( 3 | sin ⁡ t | + 9 cos 2 ⁡ t + 3 sin ⁡ t , 9 sin 2 ⁡ t - 5 cos ⁡ t + 2 ,   2 + cos ⁡ t + 3 sin ⁡ t ) ⋅ ( - 3 sin ⁡ t ,   - 3 cos ⁡ t ,   2 sin ⁡ t )   d t =

= ∫ 0 2 π - 27 cos 2 ⁡ t sin ⁡ t - 9 sin ⁡ t sin ⁡ t + sin ⁡ t - 27 sin 2 ⁡ t cos ⁡ t + 15 cos 2 ⁡ t - 6 cos ⁡ t + 4 sin ⁡ t + 2 sin ⁡ t cos ⁡ t + 6 sin 2 ⁡ t   d t

= ∫ 0 2 π - 27 cos 2 ⁡ t sin ⁡ t - 9 sin ⁡ t | sin ⁡ t | - 27 sin 2 ⁡ t cos ⁡ t + 9 ( cos 2 ⁡ t - sin 2 ⁡ t ) - 6 cos ⁡ t + 4 sin ⁡ t + 2 sin ⁡ 2 t + 6   d t

= ∫ 0 2 π - 27 cos 2 ⁡ t sin ⁡ t - 9 sin ⁡ t | sin ⁡ t | - 27 sin 2 ⁡ t cos ⁡ t + 9 cos ⁡ 2 t - 6 cos ⁡ t + 4 sin ⁡ t + 2 sin ⁡ 2 t + 6   d t

Resposta

∫ 0 2 π - 27 cos 2 ⁡ t sin ⁡ t - 9 sin ⁡ t | sin ⁡ t | - 27 sin 2 ⁡ t cos ⁡ t + 9 cos ⁡ 2 t - 6 cos ⁡ t + 4 sin ⁡ t + 2 sin ⁡ 2 t + 6   d t

Exercícios de Livros Relacionados

Uma curva, denominada bruxa de Maria Agnesi, consiste em todas as possíveis posições possíveis do ponto P na figura. Mostre que as equações paramétricas para essa curva podem ser escritas como x = 2 a
Deduza as Equações I para o caso π 2θπ .OBS:As equações I são as equações paramétricas do cicloide dadas por x = r ( θ - sen ⁡ θ ) y = r ( 1 - cos ⁡ θ ) θ ∈ R
Seja P um ponto a uma distância d do centro de um círculo de raio r . A curva traçada por P quando o círculo gira sobre uma reta é chamada trocoide. (Pense no movimento de um ponto sobre um raio de um
Identifique as simetrias das curvas nos Exercícios 1-12. Em seguida, esboce as curvas. r = 1 + cos ⁡ θ
Identifique as simetrias das curvas nos Exercícios 1-12. Em seguida, esboce as curvas. r = 2 - 2 cos ⁡ θ