Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica
Ver TeoriaEnunciado
Um anel de peso está preso a uma mola e desliza sem atrito num fio circular situado num plano vertical, conforme a figura.
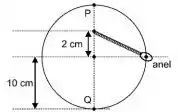
Considerando que a mola não se deforma quando o anel se encontra na posição e que a velocidade do anel seja a mesma nas posições e , a constante elástica da mola deve ser de:
Passo 1
DEUS DU CÉU, VISHI MAINHA, OH MY JESUS, QUE QUI TA ACONTECENU AQUI.
Calma filho, ta tudo calmo, ta tudo 2. O que ta acontecendo aqui é que nós temos um anel que fica rodando nesse círculo ai e tem uma mola presa ali. Alí ó , naquele pontinho ali! Ela não sai dali, sacou?
E olha que maneiro, o que ta variando direto ali é a velocidade, mas em dois pontos o problema falou que a velocidade é igual! Vamos usar esses dois pontos pra ficar mais fácil, pode ser?
Além disso, vamos usar esses dois pontos porque novamente não tem forças dissipativas atuando no anel. Se não tem, é só conservar energia nos dois pontos que ta tudo tranquilo.
Vamos usar o ponto como referência, fechou?
Passo 2
Calculando a energia no ponto :
Lembrando que como a mola não está deformada no ponto , a mola tem comprimento de cm. O que importa aqui é a variação!!
Passo 3
Calculando a energia no ponto P:
Passo 4
Fica atento ali nas unidade , ein? Sempre temos que trabalhar em metros!!!
Como sabemos que os dois tem a mesma energia, vamos igualar as duas equações que achamos e encontramos o valor de !