Um pêndulo está suspenso do teto e preso a uma mola que, por sua vez, está presa ao chão em um ponto diretamente abaixo do suporte do pêndulo. A massa da bolinha do pêndulo é , o comprimento do pêndulo é e a constante da força é . O comprimento da mola frouxa é e a distância entre o chão e o teto é . O pêndulo é puxado lateralmente, de modo a formar um ângulo com a vertical e é então liberado do repouso. Obtenha uma expressão para a rapidez da bolinha, quando ela passa pelo ponto diretamente abaixo do suporte do pêndulo.

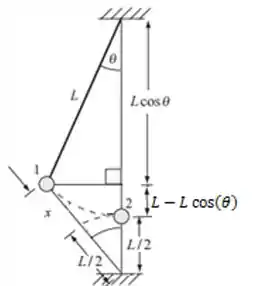
Vamos escolher o ponto mais baixo da trajetória como sendo . O que vai acontecer na questão é que a energia gravitacional e a energia elástica que a bolinha possui no ponto vai ser transformada em energia cinética quando chegar no ponto .

Vamos conservar energia nos dois pontos (olha, mais uma vez!) porque não temos forças dissipativas atuando na bolinha.

Pra descobrir a deformação da mola temos que aplicar Pitágoras no triângulo de baixo, só que não temos o cateto horizontal. E como acha? É só aplicar Pitágoras no triângulo de cima! Vamos chamar esse cateto de

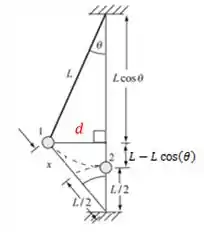
Assim

Eu sei que você quer tirar a raiz quadrada desse valor aí mas não precisa por que quando formos usar o teorema de Pitágoras no triângulo de baixo vai aparecer também!

Agora vamos olhar o triângulo de baixo. Pra facilitar a vida, vamos reescrever o cateto vertical como

Assim, aplicando Pitágoras

Substituindo do passo anterior

Agora vamos desenvolver esse bicho feio. Primeira coisa é botar em evidência

Agora vamos abrir o quadrado no final da expressão

O vai embora e ficamos com

Agora sim podemos tirar a raiz dos dois lados

Isolando e botando em evidência

Agora que já sabemos a deformação da mola, podemos comparar a energia mecânica nos dois pontos

Como queremos saber a velocidade

Substituindo os valores que a gente conhece na equação temos:

Isolando a velocidade ficamos com:

Eu falei que os números eram não muito bonitos ... hahahhaha