Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica

Ver Teoria
Exercício 571234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556585960616263646566

Enunciado

Energia Potencial e Conservação da Energia

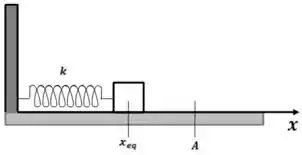
Um pequeno bloco de massa m está sobre uma superfície horizontal sem atrito ligado a uma mola de constande elástica k cuja outra extremidade é fixa em uma parede, como mostra a figura. O bloco é deslocado para x = A , a partir da posição de equilíbrio, x e q = 0 e liberado a partir do repouso. Para qualquer instante posterior, o módulo da sua velocicade é dado por:

  1. v = k m ( A 2 - x 2 )
  2. v = k 2 m ( A 2 - x 2 )
  3. v = 2 k m ( A 2 - x 2 )
  4. v = k / m x
  5. v = k / m A

Passo 1

Os dados do enunciado são

D a d o s m k A

Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.

Como não temos atrito, não temos trabalho sendo feito então

E m A = E m p o n t o   q u a l q u e r

Passo 2

Temos

E m A = U e l

E m A = k Δ x 2 2

Onde

Δ x = A - 0 = A

Que foi o quanto a mola ficou deformada.

Então

E m A = k A 2 2

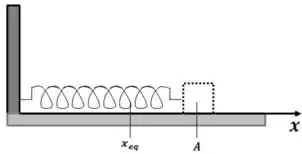
Passo 3

E m p o n t o   q u a l q u e r = U e l + K

Onde

U e l = k Δ x 2 2

Com

Δ x = x - 0 = x

Que foi o quanto a mola ficou deformada em um ponto x qualquer. Além disso,

K = m v 2 2

Passo 4

Teremos então

k A 2 2 = k x 2 2 + m v 2 2

v 2 = k A 2 - x 2 m

v = k A 2 - x 2 m

Resposta

Letra A

Exercícios de Livros Relacionados

A Fig. 8-39a se refere à mola de uma espingarda de rolha (Fig. 8-39b); ela mostra a força da mola em função da distensão ou compressão da mola. A mola é comprimida 5,5c m e usada para impulsionar uma
Uma mola com uma constante elástica de 3200N / m é distendida até que a energia potencial elástica seja 1,44J . ( U = 0 para a mola relaxada.) Quanto é ∆ U se a distensão muda para (a) uma distensão d
Verdadeiro ou falso (a partícula desta questão pode se mover somente ao longo do eixo x e está submetida a uma única força, e U(x) é a função energia potencial associada a esta força.):(a) A partícula
Verdadeiro ou falso (a partícula desta questão pode se mover somente ao longo do eixo x e está submetida a uma única força, e U(x) é a função energia potencial associada a esta força.):(a) A partícula
Em uma erupção vulcânica, um pedaço de 2k g de um rocha vulcânica porosa é jogada diretamente para cima com uma rapidez inicial de 40m / s . Ela viaja por uma distância de 50m antes de começar a cair