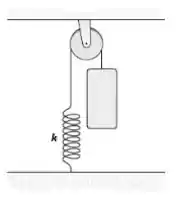
Um bloco de massa está preso por um fio a uma mola de constante elástica . O fio passa por uma polia de cujo momento de inércia em relação ao seu eixo de rotação é . O fio tem massa desprezível, é inextensível e não desliza sobre a polia, que pode girar sem atrito em torno do seu eixo de rotação. O bloco é liberado em repouso e com a mola relaxada. Qual é a rapidez do bloco depois de ter caído ?
(A)(B)(C)(D)(E)
Passo 1
Fala aí meus lindos e lindas! Tudo bem com vocês? Bora pra cima! Na questão acontece um movimentinho interessante: esse bloco (pela ação da gravidade) vai descendo e através daquela corda, tensiona a mola. Ou seja, temos um cenário no começo do problema (que é essa da figura) e temos outro cenário depois do movimento. Para o estado inicial:
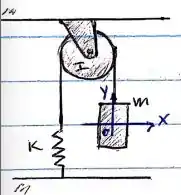
Agora, o estado de interesse, que é a velocidade do bloco em uma certa altura que a questão pede:
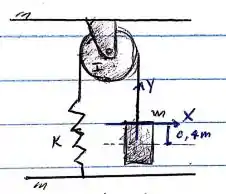
Sacaram o problema? Então, sem mais delongas bora lá encontrar a velocidade depois que o bloco passa da altura inicial dela. Pra essa tô animado!

Passo 2
Agora, precisamos escrever o problema em uma equação pra descobrir o que a gente quer. Você sabe qual método vamos adotar? Qual fórmula, lei ou teorema? Então, se você disse conservação de energia, você acertou em cheio as somas das energias cinéticas e potenciais no começo do movimento é igual a soma das energias cinéticas e potenciais no final do movimento. Sendo assim, vamos escrever exatamente o que está em negrito aqui em baixo:
(1)
e são respectivamente energia cinética e potencial. E as letrinhas pequeninas ali em baixo “ e ” indicam respectivamente o estado inicial e o estado final (ou de interesse pro nosso caso).
Passo 3
Passo 4
Agora vamos imaginar esse momento inicial onde tá tudo parado. Temos a mola relaxada, e o bloco ainda não começou a cair, ele ainda está em uma altura . Agora vamos dar play no movimento! O que aconteceu? O bloco está caindo, a polia está girando. Opa, vejam só!!!

Acabamos de encontrar as duas energias cinéticas que acontecem no sistema. Bora procurar as energias potenciais? Perceba que se o bloco caiu, além dele se movimentar ganhando energia cinética, pelo fato de estar caindo, vamos ter no sistema energia potencial gravitacional. E pra gente finalizar tá faltando mais uma energia aqui, você sabe qual é? Justamente a da mola. Ela representa uma energia potencial elástica. Fechou, agora no próximo passo vamos jogar as fórmulas de cada energia na equação .
Passo 5
Como foi dado o spoiler no passo anterior, vamos jogar tudo isso que tá em negrito na equação . Ela é representada por:
Para as energias cinéticas e potenciais iniciais, temos:
Mas veja, se a velocidade inicial é , e a altura inicial é também, temos no final isso:
Logo,
(2)
Até aqui tudo bem, agora vamos pro estado de interesse. Do outro lado da equação temos:
De energias cinéticas, como a gente descobriu no passo , temos que o bloco cai, e a polia gira. Isso é traduzido em energia cinética do bloco caindo, e em energia cinética rotacional da polia girando. Logo, temos essas fórmulas:
(3)
Para as energias potenciais, temos a energia potencial gravitacional pela ação do bloco cair, e a energia potencial elástica pela ação da mola esticar do outro lado da polia. Portanto:
(4)
Agora que temos tudo esquematizado, vamos juntar todas as equações no próximo passo e arrematar a questão.
Passo 6
Juntando as equaçõese nos moldes da equação , temos:
E mais uma coisita: como adotamos o sentido de para cima ser positivo, e o bloco desce (para baixo), significa que ele perde altura. Ou seja, a variação dele é igual a:
Belezinha? Prontos pra substituírem esses valores? A questão nos entrega:
Agora só tá faltando o quanto que a mola estica e transformar aquele da energia cinética rotacional da polia em algo que a gente possa trabalhar. Primeiro resolvendo o problema da mola, o problema nos entrega que o fio é inextensível e não desliza. O que isso significa pra gente? Significa que toda variação de altura no bloco, é transferida totalmente pra polia que é transferida totalmente para a mola. Se o bloco desceu , a mola estendeu os mesmos . Logo,
Para o nosso , podemos traduzir ele na forma da velocidade de giro, que é dada por:
Logo,
Agora substituindo tudo isso na nossa equação (5):
Isolando essa velocidade, temos que:
alternativa c)
E é isso! WE DID IT!!! Se ficou alguma dúvida, quer dar alguma sugestão ou reportar algum erro, manda um feedback pra gente! Vamos adorar ajudar você
Passo 7
Resposta
alternativa c)