Um trenó com um passageiro tem massa total (trenó + passageiro) de e percorre uma colina congelada perfeitamente lisa como mostrada na figura abaixo. Em que ponto o trenó “aterrissará”, em relação a base do penhasco (cliff)?
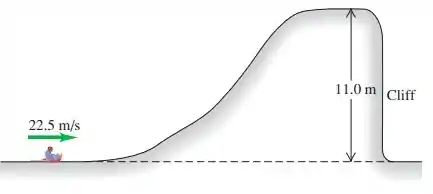
Passo 1
Falaaa, meu povo lindo!! Quais as novidades por aí, além de que o Responde Aí tá te deixando suuuper confiante nas matérias?? Hmm, então bora ficar em mais uma, com essa questão??
Temos um trenó com um passageiro que sobe uma colina congelada. Após passarem pela parte mais alta dessa colina, iniciam um movimento semelhante ao lançamento oblíquo. 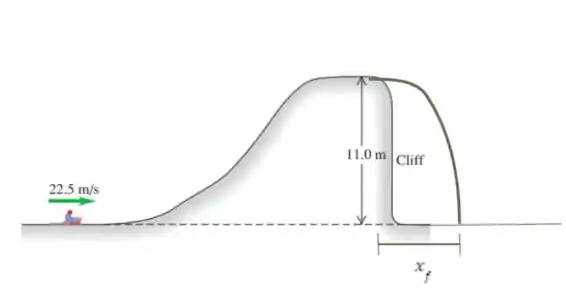
Esse trenó, juntamente com o passageiro, voltam para o chão e devemos encontrar a que distância do penhasco em que ocorre essa aterrissagem.
Como resolver essa questão???
Considerei o instante inicial, o momento em que o trenó ainda está no solo e o instante final o momento em que o trenó se encontra na parte mais alta do penhasco.
Passo 2
Vamos utilizar a conservação de energia com o intuito de descobrir a velocidade do trenó no topo do penhasco.
Como o trenó parte do nosso referencial, isso quer dizer que a energia potencial no instante inicial será zero.
Perfeito! Então aqui obtemos a velocidade horizontal do trenó quando ele se encontra no ponto mais alto da colina. Agora precisamos analisar o movimento de “queda” desse trenó.
Passo 3
Então, vamos comparar a descida da parte mais alta da colina como um movimento de lançamento oblíquo.
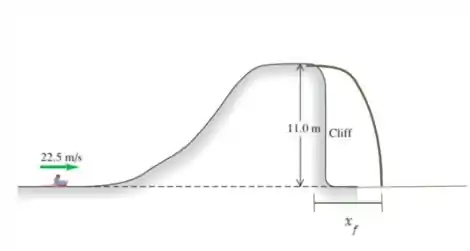
Bom, antes de começar de fato a trajetória paraboloide, a velocidade inicial em relação ao eixo é nula.
Adotando o eixo positivo para cima e o eixo para a direita.
Então, acabamos de encontrar quanto tempo o trenó demorou para aterrissar no chão.
Passo 4
Vamos analisar agora o movimento de “queda” na horizontal.
Utilizando a fórmula do alcance para o lançamento oblíquo:
Como estamos interessados no quanto o trenó se distanciou da base do monte Cliff, vamos considerar essa base como = 0
E sabendo que a velocidade horizontal inicial era e que o tempo de queda foi . Podemos concluir que
Assim, podemos dizer que o trenó aterrissou a da base do monte Cliff.
Resposta
O trenó aterrissará a da base do penhasco.