[ENUNCIADO COMUM ÀS QUESTÕES 3 E 4]
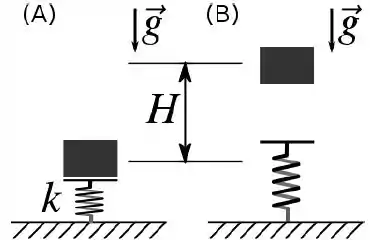
Um bloco de massa é colocado sobre uma mola, de massa desprezível e constante elástica , que possui a outra extremidade fixa em uma superfície horizontal. Na figura (A), a mola está comprimida de em relação a sua posição não deformada. A figura (B) mostra o sistema depois de ter sido liberado, com o bloco atingindo uma altura máxima em relação à sua posição inicial [na figura (A)]. Considere
[QUESTÕES 4]
Suponha agora que . Qual é a altura máxima atingida pelo bloco?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Se a deformação da mola é igual a , isso gera uma força elástica de:
E esse valor é muito maior do que a força peso:
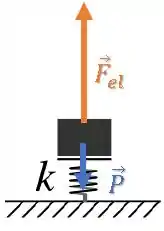
Ou seja, essa mola vai empurrar o bloco para cima de forma que ele será catapultado...
Nós queremos saber que altura ele atinge.
Passo 2
Para descobrir essa altura, poderíamos achar a aceleração no movimento de subida a partir da força resultante:

Porémmm, repara que a força da mola é variável a medida que a deformação muda.
Ou seja, precisaríamos resolver com uma integral...

É... achei que você não ia gostar muito da ideia mesmo hahha.
Então, vamos resolver a partir de energia.
Passo 3
Temos que a energia desse sistema (bloco+mola) se conserva:
Quando a mola está comprimida, toda sua energia está armazenada na forma de energia potencial elástica.
Depois, à medida que o bloco vai subindo, sua energia vai se transformando em energia potencial gravitacional.
Passo 4
Conservando a energia, temos:
Substituindo os valores numéricos:
Ficamos com a letra (f).
Resposta
Letra (f)