Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica
Ver TeoriaEnunciado
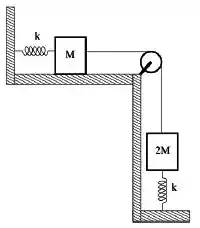
Dois blocos de massas e estão ligados por um fio inextensível e sem massa que passa por uma polia de massa desprezível. As molas têm a mesma constante elástica . Não há atrito no eixo da polia nem entre o bloco de massa e a superfície horizontal. Se os blocos são liberados a partir do repouso com ambas as molas relaxadas, qual é a distância que o bloco que está sobre a superfície horizontal percorre até parar pela primeira vez?
(A)
(B)
(C)
(D)
(E)
Passo 1
Nesse caso, não temos atrito e as forças externas, peso e elástica, são forças conservativas. Além delas, temos aquela força normal no bloco de cima, porém, ela não realiza trabalho ao longo do movimento.
Então, ufa! Mas por que eu falei isso tudo?
Porque, agora, sabemos que há a conservação de energia mecânica nesse sistema.
Mas quem são os instantes inicial e final?
Instante inical:
Os corpos estão em repouso e as molas estão relaxadas. Assim, tanto a energia cinética quanto a potencial elástica são nulas. Porém, também temos que analisar a energia potencial gravitacional .
Vamos considerar que o bloco de massa desce uma certa altura antes de atingir a deformação máxima da mola. Logo, na situação inicial, ele terá uma energia potencial gravitacional associada a essa altura .
Já o bloco de massa , vai ter uma energia potencial gravitacional também, porém, como ele não varia sua altura ao longo do movimento, ela vai se manter constante e cortar dos dois lados da equação.
Então, a energia mecância inical é:
Instante final:
Novamente os dois blocos estarão em repouso, pois a ação da mola os parou. Então, a energia cinética é nula novamente.
Como já dito antes, o bloco de massa continuará com a mesma , porém o bloco de massa atinge sua altura mínima, logo ele terá uma energia potencial gravitacional nula.
Não podemos nos esquecer das molas, que ao se deformarem acumularam energia potencial elástica.
Se antes elas estavam relaxadas, quando o bloco de massa desce uma altura , a deformação dessa mola será exatamente igual à essa altura.
Mas e o bloco na horizontal?
Ele terá um certo deslocamento horizontal que será igual à deformação da mola de cima:
Mas, como ele está conectado ao outro por um fio inextensível, seus deslocamentos devem ser iguais. Por isso, temos que:
A energia mecânica será:
Passo 2
Agora é só jogar na equação de conservação da energia mecânica que conseguimos esse valor do deslocamento.
Cortando , temos:
Como os valores de e de são iguai:
Ficamos com a alternativa (B).
Resposta
Letra (B)