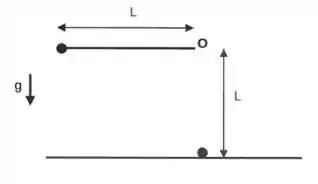
Uma bolinha de massa m está presa a uma das extremidades de uma haste rígida de massa desprezível e comprimento . A haste pode girar livremente em torno de um eixo perpendicular passando por sua outra extremidade (ponto ). O raio da bolinha é muito menor do que o comprimento da haste. O conjunto é liberado a partir do repouso na posição horizontal e, quando passa pela posição vertical, colide com uma bolinha idêntica em repouso. Não há atrito entre a bolinha e a superfície horizontal sobre a qual está apoiada. As bolinhas grudam uma na outra durante a colisão. Qual é a velocidade angular do sistema imediatamente após a colisão?

Vamos agora entender o que acontece com e depois da colisão. Imediatamente no momento em que elas se colidem, o sistema que a gente vai observar agora é formado poelas duas bolas. O sistema agora tem massa como mostrado no esquema a seguir:

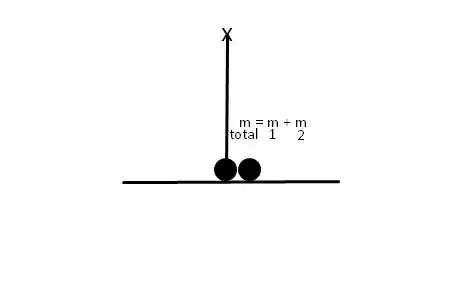
Nesse caso para :

E para para :

Para:

E do método de conservação dos momentos lineares

Agora, vamos voltar e aplicar na nossa formula do passo passado do método de conservação dos momentos lineares:

Para o nosso sistema:

Resolvendo:

E pra gente finalizar, vamos achar a velocidade angular. Ela é dada por:

Mas, achamos no passo anterior que:

Logo,

E que:

Logo, substituindo em :

E é isso turminha! Se ainda restou alguma dúvida manda um feedback pra gente que vamos adorar te ajudar! Até a próxima questão e bons estudos