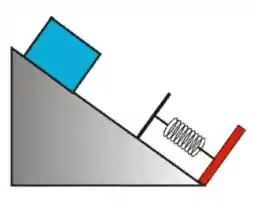
Um bloco de massa é solto, a partir do repouso, em um plano inclinado de em relação à horizontal, com coeficiente de atrito cinético . Depois de percorrer uma distância de ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava inicialmente relaxada, de acordo com o esquema mostrado na figura ao lado.
b) Qual a energia dissipada pelo atrito durante o trajeto do bloco desde o alto do plano até a compressão total da mola? Essa energia dissipada corresponde a que fração da variação total de energia potencial durante o trajeto?
Passo 1
Oi oi galerinha, por aí tá tudo certo??
Vamos começar traduzinho esse enunciado aí hein! Vem comigoo!
O enunciado nos diz que um bloco de massa deslizou uma distância em um plano inclinado de , até encontrar uma mola de constante de , considerando que o bloco atritou com coeficiente de atrito cinético de . Não conseguiu imaginar? Olha o desenho do nosso probleminha...
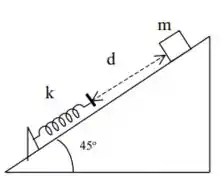
Nossa missão vai ser determinar a energia dissipada durante o atrito!
Passo 2
O segredinho para resolvermos essa questão é lembrarmos que a energia dissipada equivale a força de atrito multiplicado pelo deslocamento, logo:
Lembra que o atrito depende da força normal () e do coeficiente de atrito ()? Vem dessa fórmulinha aqui:
Passo 3
Agora basta nós substituirmos os valores:
- coeficiente de atrito é ;
- deslocamento total é , sendo a deformação da mola encontrada na item a);
- força normal equivale a decomposição de força desenhada:
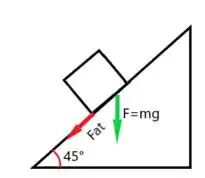
Ou sejaaa, a energia dissipada é:
Substituindo os valores:
Prontinhooo, encontramos a energia dissipada durante o atrito!