Considere um sistema de lançamento constituído por um plano inclinado de comprimento , inclinado de e uma mola de constante elástica . Uma das extremidades da mola está presa a um anteparo na base do plano. Na outra extremidade da mola apoiamos um bloco de massa a ser lançado. A mola tem massa desprezível e quando relaxada tem comprimento . Para lançar o bloco, a mola é comprimida até a partir da posição de equilíbrio e então o bloco é solto. Ele sobe plano acima até sair do plano fazendo uma trajetória parabólica. Existe atrito entre o plano e o bloco com . Resolva o problema utilizando somente considerações de energia.
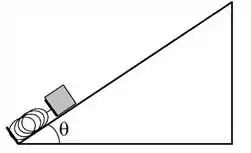
a) Determine a energia potencial elástica armazenada na mola antes do lançamento do bloco.
b) Determine a variação da energia potencial gravitacional do bloco durante a compressão da mola.
c) Suponha que quando a mola empurra o bloco plano acima, ele perde contato com a mola quando ela fica relaxada. Determine o módulo da velocidade do bloco imediatamente após ele ter perdido contato com a mola.
d) Determine a altura máxima que o bloco alcança, em relação à base do plano, depois dele ser lançado do plano inclinado numa trajetória parabólica. A velocidade do bloco na iminência de sair do plano é .
Passo 1
Vamos entender o que tá acontecendo:
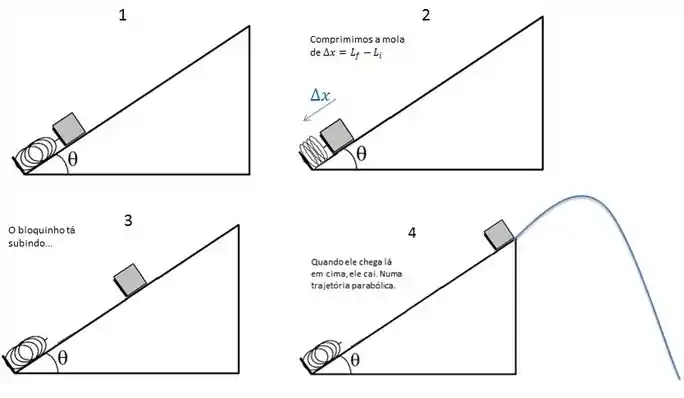
Show? Agora, vamos ver o que os dados do enunciado estão nos falando.
Passo 2
Vamos ver os dados e já colocar tudo no SI.
Passo 3
Beleza, até agora só ajeitamos as coisas... Então vamos ver o que ele quer: Energia que a mola armazenou quando ela é comprimida pelo bloco.
Como não existem forças dissipativas roubando energia do nosso sistema (não tem atrito, nem outra força dissipativa), a energia mecânica se conserva!!
Vamos fazer a conservação da energia entre os pontos 1 e 2 lá da figura do passo 1.
Beleza? Partiu pra próxima então.
Passo 4
b) O bloco empurra a mola, certo? Então tem uma variação na altura dele em relação ao chão.
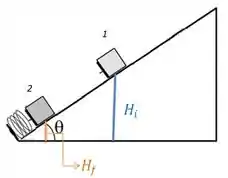
Dei uma exagerada aí nas alturas pra gente poder ver melhor. Mas a ideia é calcular a variação de entre essas alturas aí.
Pergunta: Conhecemos essas alturas?
Resposta: Não...Ainda. Vamos achar elas agora
Passo 5
Acompanha comigo pra gente achar as alturas:
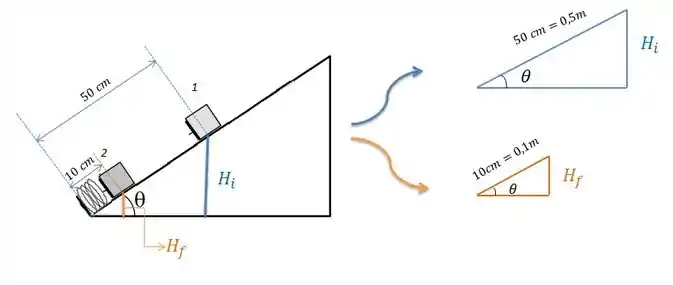
A gente tem dois triângulos, o de altura (triângulo azul), e o de altura (triângulo laranja). Vamos calcular o seno do ângulo . Ah, vou usar a medida da hipotenusa em metros, ok? E lembrando que o
Pronto, já sabemos quem são as alturas. Agora vamos substituir esses valores lá na equação de energia potencial.
Passo 6
Tem que colocar os valores com as unidades de e para que a energia tenha unidade de
Show! Próxima!
Passo 7
c)
Agora ele quer saber a velocidade assim que o bloco solta a mola.
A gente pode fazer por conservação de energia mecânica?
NÃO!
Por que?
Porque tem o atrito!! A força de atrito é uma força dissipativa, que está roubando energia do nosso sistema.
Ah, beleza...então o que a gente pode fazer?
Quando temos uma força dissipativa tirando energia do sistema, temos que a variação da energia mecânica é igual ao trabalho realizado por essa força dissipativa, mas calma!
É só isso:
Agora, vamos ver os pontos em que temos que calcular essas energias:
Passo 8
Na posição 1, a mola está comprimida (calculamos isso na letra a) e o bloquinho em repouso (velocidade é zero) além disso, o bloquinho está a uma altura .
Na posição2, a mola já tá relaxada (energia potencial elástica é nula), o bloquinho tá a uma altura , e a velocidade neste ponto é o que queremos saber!
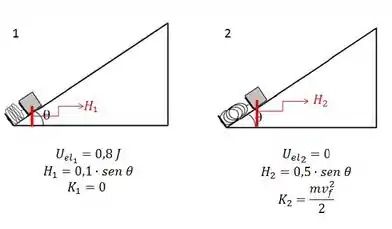
Beleza?
Então vamos olhar primeiro para o lado direito da equação do passo 7:
Pronto, já temos o resultado do lado direito.
Vamos pro lado esquerdo.
Passo 9
Vamos calcular o trabalho da :
O deslocamento é o quanto nós comprimimos a mola, que vale . A força de atrito e o deslocamento estão em sentidos opostos, então o .
E a . Vamos fazer um diagrama de força pra encontrar essa normal:

Então a normal vale
Beleza?
Agora já podemos calcular o trabalho da força de atrito:
Passo 10
Agora é só colocar os valores lá na equação do passo 7.
Já tá acabando! Vamos pra última
Passo 11
d)
Ele quer saber a altura máxima que o bloquinho alcança depois de ser lançado do plano inclinado
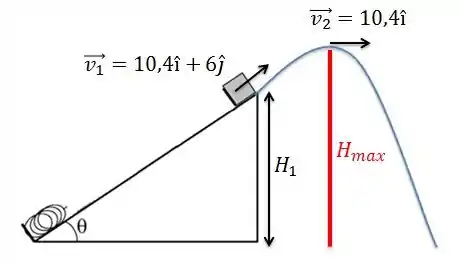
Agora o bloquinho já não está mais em contato com a superfície, então não temos atrito!!Logo a energia mecânica se conserva.
Ah, só mais uma coisa...Nessa figura eu já escrevi as velocidades nos pontos 1 e 2.
A velocidade 1 é dada, e a 2 tem a componete nula porque o bloquinho já atingiu a altura máxima..ele não vai mais subir. Momentaneamente a velocidade na vertical é nula, aí o bloquinho começa a descer. E em é um movimento uniforme, então ela não vai mudar. Beleza?
Passo 12
Para descobrirmos a altura vamos fazer a mesma coisa que já fizemos um milhão de vezes nesse exercício. Calcular o seno do ângulo. Lembrando que o comprimento do plano inclinado é 1m.
Passo 13
A gente vai fazer a conservação da energia mecância. Então precisamos do módulo do vetor velocidade! (Afinal, energia não é uma grandeza vetorial!!!)
Agora que já temos tudo, vamos fazer a conservação da energia:
Resolvendo isso:
Passo 14
Passo 15
Passo 16
Resposta
a)
b)
c)
d)