Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica
Ver TeoriaEnunciado
Dois blocos de massas e estão presos a uma mola de constante elástica que tem uma das extremidades fixa, como mostra a figura. Não há atrito entre o bloco e a superfície horizontal nem no eixo da polia, cuja massa é desprezível. Os blocos são liberados a partir do repouso com a mola relaxada. Qual é a energia cinética do bloco que está pendurado depois de ter descido ?
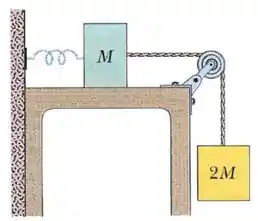
(A) 0,45 J
(B) 0,90 J
(C) 1,8 J
(D) 2,7 J
(E) 3,6 J
Passo 1
Temos aqui que no começo a mola está relaxada e que os blocos partem do repouso. No começo não temos energia potencial elástica e nem cinética e vamos setar a energia potencial gravitacional do bloco de massa para . Assim temos que a energia mecânica inicial é
Para descobrir a energia cinética do bloco da direita temos que achar a sua velocidade!
Passo 2
Como os dois blocos estão presos por um fio, temos que o quanto um deles se deslocar o outro irá deslocar também, ou seja, conforme o bloco da direita vai descendo o bloco da esquerda irá mais para a direita esticando a mola!
Também temos que os dois blocos terão mesma velocidade já que estão conectados pelo fio!
Beleza, beleza, vamos usar essas informações para amarra tudinho! o/
Passo 3
Depois do da direita ter descido temos que este bloco tem uma energia potencial gravitacional de
Já o bloco da esquerda ganha energia elástica dada por
Já os dois blocos agora têm cada um uma velocidade , de forma que a energia cinética total é dada por
Assim a energia mecânica final é dada por
Passo 4
Usando a conservação de energia mecânica temos
Isolando
Substituindo os valores dados pelo enunciado temos
Em unidade do SI. Eu não tirei a raiz quadrada por preguiça, por que só preciso fazer
Resposta
(C)