Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica
Ver TeoriaEnunciado
Conservação de Energia Mecânica
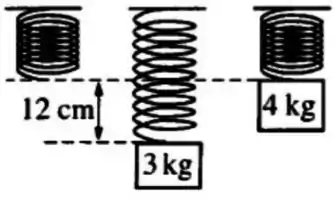
Um bloco de massa é pendurado em uma mola, fazendo com que o seu ponto de equilíbrio se desloque centímetros, como mostrado na Figura. O bloco de é então substituído por um bloco de , e o novo bloco é solto partir da posição representada, na qual a mola não está esticada nem comprimida (ponto de equilíbrio). Até aonde o bloco de vai cair antes que se inverta o sentido do movimento?
a)
b)
c)
d)
e)
Passo 1
Vamos usar primeiro o bloco de para calcular a constante elástica da mola.
Como o bloco de está pendurado na mola, vamos assumir que ele esteja em repouso, então as força resultante sobre o bloco deve ser nula. Isso nos dá que a força elástica tem que anular a força peso.
Substituindo os valores dados:
Passo 2
Agora utilizando o bloco de , vamos aplicar a conservação e energia mecânica.
Onde:
O objeto é solto do repouso e a partir da posição de equilíbrio, logo .
Além disso, na posição final onde ele está na iminência de inverter o movimento o bloco vai ter velocidade nula, e sua energia potencial elástica será máxima, ou seja, toda a energia potencial gravitacional terá se convertido em energia potencial elástica, logo .
Ficamos então com:
Obs: estamos medindo a energia potencial gravitacional tomando como a diferença de altura já que não sabemos a distância até o solo.
Simplificando a equação ficamos com:
Substituindo os valores:
Resposta
Alternativa .