Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica

Ver Teoria
Exercício 261234567891011121314151617181920212223242527282930313233343536373839404142434445464748495051525354555657585960616263646566

Enunciado

Um bloco de massa m inicialmente em repouso desliza para baixo em um plano inclinado que faz um ângulo θ com a horizontal. Depois de ter deslizado uma distância d , o bloco colide com uma mola de constante elástica desconhecida. A mola reduz a velocidade do bloco até fazê-lo parar momentaneamente. Neste instante a mola está comprimida de uma distância x . Não existe atrito entre o plano e o bloco até o contato com a mola (deslocamento d ). Mas existe atrito entre plano e o bloco na região da mola (deslocamento x ) com coeficiente de atrito cinético μ . Use g para a aceleração da gravidade. Responda em função dos dados fornecidos utilizando a Lei de Conservação de Energia.

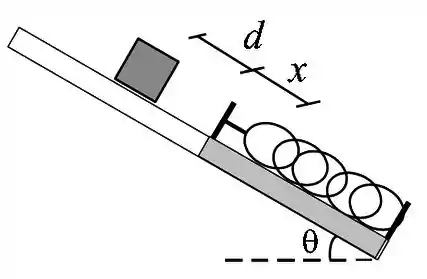
(a) Determine a energia cinética que o bloco possui na iminência de colidir com a mola, em função das variáveis.

Passo 1

Conservação da energia mecânica

A letra ( a ) nada mais é do que um problema de conservação da energia mecânica. Mas espera, porque? Calma, é simples: toda vez que não tivermos forças dissipativas, isto é, atrito, podemos falar de conservação da energia mecânica. E veja que a mola não passou por regiões com atrito nesse primeiro momento! Temos então:

∆ K +   ∆ U g +   ∆ U e l = 0

Passo 2

Cortar a(s) parcela(s) que não temos

Bem, nem todas as parcelas da conservação vão contar nesse caso! Então fique atento porque do repouso até a iminência de tocar na mola, a própria mola não entra em questão. Logo, a parcela de variação da energia potencial elástica a gente vai cortar, beleza?

∆ K +   ∆ U g +   ∆ U e l = 0

∆ K = -   ∆ U g

Passo 3

Calcular a energia cinética

Já que temos uma relação pra energia cinética, vamos usá-la! Mas fica ligado porque tem mais simplificações pra fazer nela. Por exemplo, como inicialmente o bloco está em repouso, a energia cinética inicial tem que ser 0. Ou seja:

∆ K = -   ∆ U g

K f - K i = m g h i - h f

K f = m g ∆ h

Opa, mas quem é esse ∆ h que surgiu do nada? Essa é a diferença de altura do bloco no repouso até tocar na mola. A gente não sabe qual é o seu valor, mas por trigonometria, conseguimos mudar sua expressão:

∆ h = d . s e n   θ

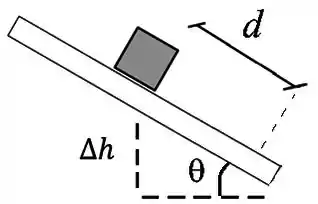
Agora sim a gente tem tudo pronto pra escrever a energia cinética no final desse movimento. Ela vai ser:

K f = m g d . s e n   θ

Resposta

  1. K f = m g d . s e n   θ  

Exercícios de Livros Relacionados

A Fig. 8-39a se refere à mola de uma espingarda de rolha (Fig. 8-39b); ela mostra a força da mola em função da distensão ou compressão da mola. A mola é comprimida 5,5c m e usada para impulsionar uma
Uma mola com uma constante elástica de 3200N / m é distendida até que a energia potencial elástica seja 1,44J . ( U = 0 para a mola relaxada.) Quanto é ∆ U se a distensão muda para (a) uma distensão d
Verdadeiro ou falso (a partícula desta questão pode se mover somente ao longo do eixo x e está submetida a uma única força, e U(x) é a função energia potencial associada a esta força.):(a) A partícula
Verdadeiro ou falso (a partícula desta questão pode se mover somente ao longo do eixo x e está submetida a uma única força, e U(x) é a função energia potencial associada a esta força.):(a) A partícula
Em uma erupção vulcânica, um pedaço de 2k g de um rocha vulcânica porosa é jogada diretamente para cima com uma rapidez inicial de 40m / s . Ela viaja por uma distância de 50m antes de começar a cair