Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica

Ver Teoria
Exercício 111234567891012131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566

Enunciado

Um objeto de massa m , que parte do repouso, desliza sobre um plano inclinado e posteriormente percorre uma pista circular vertical de raio R , conforme ilustrado na figura abaixo. Durante todo o movimento, o atrito sobre o objeto é desprezível. Qual o menor valor possível para y (ver figura abaixo) para que o objeto percorra a trajetória circular sem nunca perder contato com a pista?

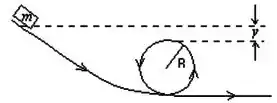
(A) R / 4

(B) R / 2

(C) R

(D) 2 R

(E) zero

Passo 1

Temos que no topo da pista circular que a força centrípeta seja dada por

F C P = m g + N

Para que o objeto não perca contato é necessário que a normal seja maior ou igual a zero, ou seja,

N ≥ 0 → F C P - m g ≥ 0

F C P ≥ m g

Por outro lado, a força centrípeta é dada por

F C P = m v 2 R

Ou seja

m v 2 R ≥ m g

v 2 ≥ R g

A velocidade tem que ser suficiente para satisfazer a condição acima.

Passo 2

Por conservação da energia mecânica temos que a energia mecânica no começo do movimento é igual à energia mecânica no topo do círculo, ou seja

E 0 = E t o p o

U 0 + K 0 = U t o p o + K t o p o

m g y + 2 R + 0 = m g 2 R + 1 2 m v 2

v 2 = 2 g y

Substituindo na condição do item anterior, temos

v 2 ≥ R g → 2 g y ≥ R g

y ≥ R 2

Resposta

(B)

Exercícios de Livros Relacionados

A Fig. 8-39a se refere à mola de uma espingarda de rolha (Fig. 8-39b); ela mostra a força da mola em função da distensão ou compressão da mola. A mola é comprimida 5,5c m e usada para impulsionar uma
Uma mola com uma constante elástica de 3200N / m é distendida até que a energia potencial elástica seja 1,44J . ( U = 0 para a mola relaxada.) Quanto é ∆ U se a distensão muda para (a) uma distensão d
Verdadeiro ou falso (a partícula desta questão pode se mover somente ao longo do eixo x e está submetida a uma única força, e U(x) é a função energia potencial associada a esta força.):(a) A partícula
Verdadeiro ou falso (a partícula desta questão pode se mover somente ao longo do eixo x e está submetida a uma única força, e U(x) é a função energia potencial associada a esta força.):(a) A partícula
Em uma erupção vulcânica, um pedaço de 2k g de um rocha vulcânica porosa é jogada diretamente para cima com uma rapidez inicial de 40m / s . Ela viaja por uma distância de 50m antes de começar a cair