Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica
Ver TeoriaEnunciado
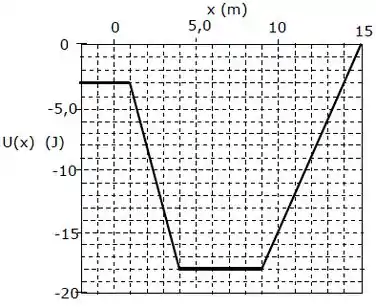
O gráfico abaixo mostra a energia potencial em joules associada à força conservativa que age sobre um corpo de massa . Quando o corpo está em sua velocidade é . Quando o corpo passa pela posição é correto afirmar que sua energia cinética é:
(A)
(B)
(C)
(D)
(E)
Passo 1
O enunciado diz que a força é conservativa, ou seja, ela não faz o sistema perder energia.
Então, podemos trabalhar com a conservação da energia mecânica.
Temos dois tipos de energia para analisar, a cinética e a potencial , mostrada no gráfico. O instante inicial será quando a partícula estiver em e o instante final será quando a partícula estiver em .
Queremos encontrar a energia cinética final :
Passo 2
Precisamos achar o valor de e .
Dentro do gráfico, na escala vertical,cada quadradinho vale e, na escala horizontal, cada quadradinho vale . Então:
Agora, podemos suabstituir os valores de , de velocidade e de massa na expressão para encontrar a energia cinética em :
Ficamos com a alternativa (D)
Resposta
Letra (D)