Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica
Ver TeoriaEnunciado
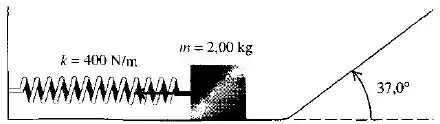
Um bloco de é empurrado contra uma mola de massa desprezível e constante , comprimindo a mola até uma distancia igual a . Quando o bloco é libertado, ele se move ao longo de uma superfície horizontal sem atrito e sobre um plano inclinado de . a) Qual a velocidade do bloco enquanto ele desliza ao longo da superfície horizontal depois de abandonar a mola? b) Qual a distancia máxima que ele atinge ao subir o plano inclinado até parar antes de voltar para a base do plano?
Passo 1
a)
Como não temos atrito atuando vamos ter a conservação da energia mecânica. Precisamos calcular a energia mecânica inicial, quando a mola está comprimida. A única energia é a potencial elástica porque ele está parado e vamos considerar a altura inicial como zero.
Passo 2
Vamos agora calcular a energia final, quando ele ainda está na horizontal, que é quando ele solta da mola. Isso nos diz que a única energia é a cinética
Passo 3
As energias são iguais então
Passo 4
b)
Agora o que vai mudar é nossa energia final, porque vamos considerar o final quanto ele atinge a altura máxima para e volta. Isso diz que a energia final é apenas a potencial gravitacional
Passo 5
Vamos igualar a energia inicial que achamos no passo 1
Mas essa não é a distancia percorrida, essa é a altura que ele chegou. Olha a figura abaixo para entender bem a diferença.
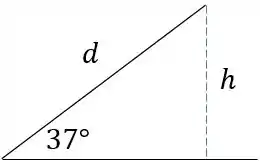
Vamos ter