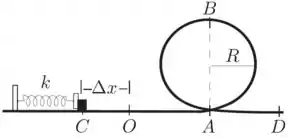
Um conhecido brinquedo consiste em uma pista contendo um “loop” circular de raio e um trecho horizontal . No ponto , localiza-se um lançador, constituído de uma mola ideal relaxada, de constante elástica . Um carrinho (representado por um pequeno bloco na figura abaixo) de massa é colocado inicialmente em . Empurra-se o carrinho, comprimindo-se a mola de até o ponto . Neste ponto o carrinho é liberado a partir do repouso perfazendo o percurso , perdendo contanto com a mola no ponto e percorrendo todo o “loop” sem perder contato com a sua superfície. Desprezando-se o atrito em todo o percurso e considerando como dados do problema:

, , , e , calcule:

1. O módulo da velocidade do carrinho ao passar por ;
2. O módulo da velocidade do carrinho ao passar por ;
3. Represente em um diagrama as forças que atuam sobre o carrinho ao passar por e determine o módulo da força de contato, , neste ponto;
4. A compressão mínima da mola para que, ao passar por , o carrinho esteja na iminência de perder o contato com o “loop”.

Como não temos forças dissipativas, vulgo força de atrito, ao longo de todo o movimento a energia mecânica se conversa. Então

a)

Vamos achar a energia mecânica do ponto e do ponto , isso porque o ponto é a partida onde temos todos os dados para encontrar a energia nesse ponto, enquanto queremos a velocidade em .

Isso porque ele é largado do repouso, e está no chão.

Isso porque ele está no chão, e sem contato com a mola.

Teremos então

b)

Vamos agora encontrar a energia mecânica no ponto

Isso porque temos a velocidade e ele está a certa altura. Igualando a energia em e a energia em temos

c)

Só temos a força normal e a força peso atuando

Ele está em um movimento circular, então

d)

Se o carrinho está na iminência de perder o contato

Usando a fórmula do item c