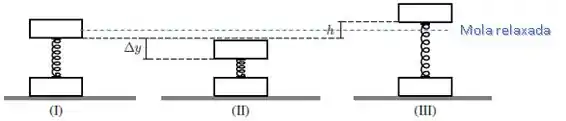
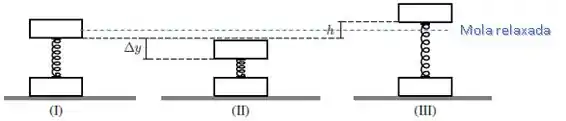
Um sistema formado por dois blocos de mesma massa , presos por uma mola de constante elástica e massa desprezível, encontra-se incialmente em repouso, apoiado sobre o chão conforme a situação () da figura abaixo.
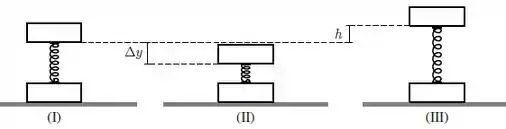
a) Em relação a seu comprimento natural, de quanto a mola está comprimida quando o sistema se encontra em equilíbrio [na situação ()]? A resposta deve ser dada em termos de , e .
b) Faça um diagrama das forças que atuam em cada um dos blocos na situação do item anterior.
c) Um agente externo empurra o bloco de cima, fazendo com que este abaixe de uma distância adicional em relação a posição de equilíbrio, conforme mostrado na situação (). Em seguida, o bloco de cima é liberado. Qual a altura máxima , em relação à posição de equilíbrio, atingida pelo bloco de cima, supondo que o bloco de baixo não perde contato com o solo [situação () da figura]? A resposta deve ser dada em termos de , , e .
d) Qual o valor máximo de para que o bloco de baixo nunca perca contato com o chão? A resposta deve ser dada em termos de , e .
Passo 1
Bom, na situação (), o sistema está em equilíbrio. Porém, equilíbrio não significa que a mola esteja relaxada.
O que acontece é que a mola está comprimida o suficiente para exercer uma força elástica que consiga equilibrar a força peso do bloco de cima:
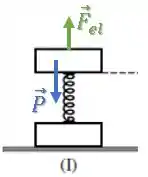
Na letra (a), queremos saber o quanto a mola está deformada para que esse bloco esteja em equilíbrio.
Como o bloco de cima está em equilíbrio:
A força elástica é dada por ( é a deformação da mola), enquanto a força peso é dada por :
Achamos então que a mola está comprimida de :
Passo 2
Na letra (b), queremos um diagrama de forças em cada um dos blocos na situação ().
Bom, já esboçamos as forças sobre o bloco de cima no Passo 1, agora temos que esboçar as forças sobre o bloco de baixo.
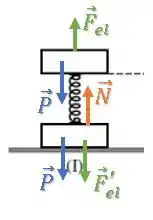
No bloco de baixo, vai existir uma força peso para baixo, uma força normal que o chão exerce sobre o bloco para cima e uma força elástica da mola comprimida empurrando o bloco:
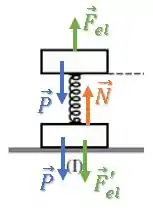
Passo 3
Na letra (c), queremos saber a altura que o bloco de cima vai alcançar depois de ser solto.
Como a força elástica é variável conforme a deformação, esse sistema vai ser mais fácil de ser analisando através de energia.
A ideia vai ser calcular a energia que o sistema tem antes do bloco ser liberado e fazer a conservação da energia para a situação de altura máxima (energia se conserva pois tanto quanto são forças conservativas).
Passo 4
Qual é a energia do sistema quando a mola está comprimida ?
Considerando um referencial de energia potencial gravitacional nulo nessa altura, a energia mecânica inicial estará toda na forma de potencial elástica:
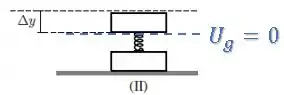
Onde é a nova deformação da mola.
Porém, muita atenção!
A mola não está comprimida apenas de .
Essa distância é a partir da posição de equilíbrio, onde a mola já está comprimida de .
Ou seja, agora a mola estará comprimida da soma dessas duas distâncias:
Passo 5
Já na situação final, a energia mecânica estará tanto na forma de potencial elástica quanto na forma de potencial gravitacional associada à altura .
Lembrando que a energia cinética é nula, pois no ponto de altura máxima a velocidade do bloco é zero.
A deformação da mola é o quanto ela está esticada com relação à posição relaxada.
Porém, temos uma distância com relação à posição de equilíbrio (mola comprimida de ).
Então, temos que subtrair de o quanto a mola estava comprimida para conseguir a real deformação da mola nesse ponto mais alto:
Então, a energia potencial elástica final será:
Já a altura a altura a partir do nosso referencial de potencial gravitacional nulo será a soma de com :
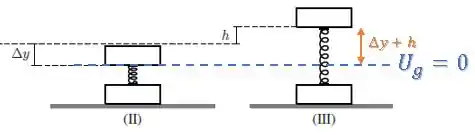
Então, a energia mecânica final é:
Passo 6
Conservando a energia mecânica, temos:
Queremos isolar , então:
Os dois termos se cancelam:
Isolando os temos com do lado esquerdo, temos:
Podemos substituir o valor conhecido para :
Os termos e os termos se cancelam cada um com seu semelhante:
Cortando , achamos que é:
Passo 7
Na letra (d), queremos saber qual o valor máximo de para que o sistema não saia do chão.
Para isso, precisamos olhar novamente para as forças, porém agora num instante onde a mola esteja esticada para cima:
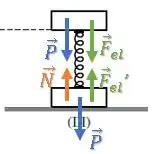
O que vai acontecer caso o sistema esteja na iminência de perder o contato com o chão?
A força normal chegará a zero, ou seja, o bloco de baixo estará prestes a sair do chão:
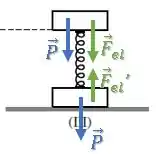
Passo 8
Assim, temos que a força elástica será igual à força peso:
Sendo a deformação da mola aquela mesma ideia que fizemos na letra (c).
Porém, também na letra (c), vimos que se a mola estiver comprimida de a partir do equilíbrio, ela subirá uma altura de mesmo valor:
Então, podemos deixar a deformação da mola em função de :
Passo 9
Substituindo isso na expressão das forças, temos:
Substituindo o valor de , temos:
Esse é o valor que a mola pode ser comprimida a partir da posição de equilíbrio para que no movimento de subida, o sistema não perca contato com o chão.
Resposta
(a)
(b)
(c)
(d)