Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica
Ver TeoriaEnunciado
PARTE I
Um bloco de massa desliza por uma rampa sem atrito com inclinação e comprimento total de iniciando o movimento a partir do repouso. Ao longo da rampa existe uma mola de constante elástica que se encontra a uma distância abaixo do bloco. O bloco atinge o repouso ao comprimir a mola de uma distância . Considere .
(a ) Escreva a equação literal para a conservação da energia mecânica para as posições inicial e final do movimento em função dos dados do problema.
(b ) Determine a compressão da mola quando a aceleração do sistema for zero.
(c ) Obtenha o módulo da velocidade máxima que o bloco alcança durante a descida.
PARTE II:
Em um salto de pára-quedas o atleta abandona o avião com velocidade vertical . Considerando a resistência do ar, sua velocidade horizontal inicial se torna nula imediatamente ao abandonar a aeronave e pode ser desprezada nos cálculos, deste modo podemos considerar uma trajetória de queda estritamente vertical. O saltador chega ao chão com velocidade
Calcule a energia total dissipada pela resistência do ar no conjunto saltador + pára-quedas. Dados: ; massa total do saltador + pára-quedas igual à ; altura inicial do avião . Use o referencial indicado com no solo.
Passo 1
Parte I
Escrevendo a equação literal para a conservação da energia mecânica
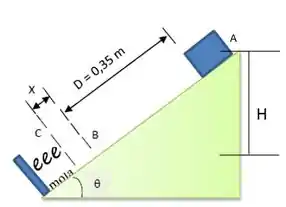
Como não há forças dissipativas atuando, podemos conservar a energia durante o movimento.
Chamaremos o alto do plano (início do movimento) de ponto A e chamaremos o ponto em que o bloco para (ponto de compressão máxima da mola) de ponto C. Consideraremos o ponto C como o referencial zero pra este cálculo.
Logo,
No ponto A teremos apenas a energia potencial gravitacional e no ponto C apenas a energia potencial elástica. Assim:
Pela trigonometria do problema, temos:
Assim, a conservação da energia com base nos dados do problema, será:
Passo 2
Determinaremos a compressão da mola quando a aceleração do sistema for zero.
Neste ponto, o equilíbrio no eixo do plano inclinado é dado por:
Substituindo os valores dados, teremos:
Passo 3
Encontrando o módulo da velocidade máximo do bloco na descida.
A velocidade máxima acontece no ponto de aceleração nula (calculado no passo anterior). Assim, utilizando o teorema Trabalho e Energia Cinética, teremos:
Passo 4
Parte II
Calcularemos a energia dissipada pela resistência do ar.
Pelo Teorema Trabalho e Energia Cinética, temos:
Na situação estudada, teremos o trabalho da força peso e o trabalho da resistência do ar atuando.
Como o saltador parte do repouso, , assim:
Logo, a energia dissipada será: