Cinco corpos, cada um de massa , estão igualmente espaçados sobre um arco de semicírculo de raio , como na Figura 11-25. Um corpo de massa está localizado no centro de curvatura do arco. (a) Se é , é e é , qual é a força gravitacional sobre a partícula de massa devida aos cinco corpos? (b) Se o corpo de massa é removido, qual é o campo gravitacional no centro de curvatura do arco?
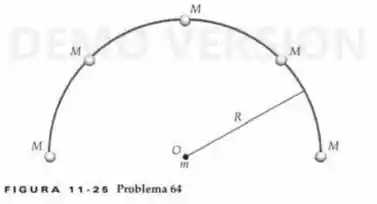
Passo 1
a) Sabemos que para encontrarmos o a força gravitacional resultante, basta somarmos vetorialmente todas as forças exercidas na massa . Se liga na figura:
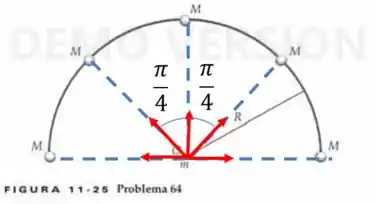
Percebe-se que todas as componentes horizontais se anulam, portanto:
Onde é a força gravitacional entre uma massa e a massa , logo:
Substituindo os valores:
Passo 2
b) Para achar o campo gravitacional, nós aprendemos a fazer o seguinte:
Portanto, o campo gravitacional NÃO DEPENDE da massa .
Então, concluímos que, podemos manter o mesmo vetor encontrado para a força, divindo-o somente pelo valor da massa :