UFPB, Sem Campus, Física Geral II, Testes de Física 2 - Profº Edvaldo Nogueira - Teste 1 - 2023.1, Questão 1
Duas esferas homogêneas de são mantidas fixas nas posições cujas coordenadas são e . Determine: o módulo, a direção e sentido da força gravitacional resultante devida a essas esferas sobre uma terceira esfera homogênea de massa igual a , situada no ponto de coordenadas , . Represente os vetores força gravitacional em termos dos vetores unitários.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu um arranjo de três partículas que exercem força gravitacional uma sobre as outras. Como elas não são colineares, não podemos simplesmente somar ou subtrair o módulo das forças exercidas pelas duas partículas sobre a terceira pra obter a força total, mas devemos usar uma soma vetorial.
Nosso arranjo, com as coordenadas dadas, é da seguinte forma:
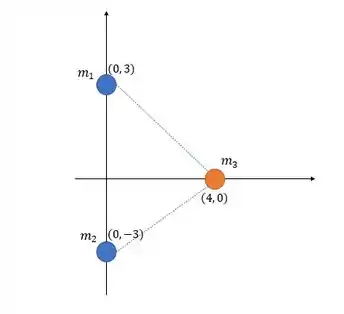
Pra determinar o módulo, a direção e sentido da força gravitacional resultante devida as esferas em azul sobre a terceira esfera em laranja, vamos calcular o módulo da força entre a esfera laranja e cada um das outras duas através da fórmula da força gravitacional:
Onde é a distância entre as esferas, e são suas respectivas massas e é a constante gravitacional igual a .
Passo 2
Repare que as forças que a partícula de massa exerce sobre as outras duas tem módulos iguais, pois a distância e a massa são as mesmas (). Sendo assim, temos:
A distância é dada pela hipotenusa do triângulo formado pelo arranjo entre as esferas, que nós vimos no passo . Assim, pelo teorema de Pitágoras, temos:
Agora podemos substituir na fórmula da força gravitacional junto com os outros dados da questão:
Esse é comprimento do vetor desenhado abaixo, assim como do outro (seu reflexo no eixo ) que representa a força gravitacional da terceira esfera sobre as outras:
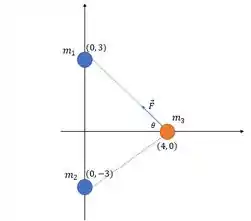
Passo 3
Perceba que as duas forças se cancelam no eixo e se somam no eixo . Por isso a força resultante terá apenas uma componente no eixo , apontando para a origem.
Vamos calcular essa componente:
Como não temos o ângulo , podemos usar a relação dos catetos sobre a hipotenusa ():
Como as forças se somam, o módulo da resultante será:
Que como vimos aponta no sentido negativo do eixo :
Prontinho, galera! Até a próxima! 😉