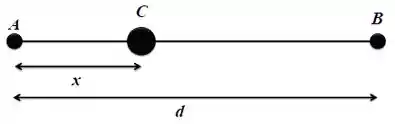
A figura ao lado mostra duas partículas puntiformes, A e B, fixadas espacialmente e separadas por uma distância d. A partícula A possui massa e a partícula B possui massa . Uma terceira partícula puntiforme deve ser colocada entre A e B. Qual o valor da distância x de modo que a partícula C esteja em equilíbrio estático apenas sob a ação das forças gravitacionais de A e B?
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
Passo 1
Para que a partícula C esteja em equilíbrio estático, a força resultante sobre ela deve ser zero!
Como a força resultante é a força gravitacional de A somada à força gravitacional de B, essa soma deve ser nula.
Então podemos escrever pra força resultante em C:
Simplificando o que dá:
A partir de agora é só conta!
Invertendo isso tudo
Resposta
Letra I.
Exercícios de Livros Relacionados
As massas e coordenadas de três esferas são as seguintes: 20k g , x = 0,50m , y = 1,0m ; 40k g , x = - 1,0m , y = - 1,0m ; 60k g , x = 0m , y =- 0,50m . Qual é o módulo da força gravitacional que as t
Qual deve ser a distância entre uma partícula de 5,2 kg e uma partícula de 2,4 kg para que a atração gravitacional entre elas tenha um módulo de 2,3 × 10 - 12 N ?
Miniburacos negros. Talvez existam miniburacos negros no universo, produzidos logo após o big bang. Se um desses objetos, com massa de 1 × 10 11 k g (e um raio de apenas 1 × 10 - 16 m ) se aproximasse
Na Fig. 13-33, três esferas de 5,00 kg estão localizadas a distâncias de d 1 = 0,300 m e d 2 = 0,400 m . Qual é (a) o módulo e (b) a orientação (em relação ao semieixo x positivo) da força gravitacion
Nos Problemas de 65 a 68, você recebe a(s) equação(ções) usada(s) para solucionar cada problema. Em cada caso, você deve: a. Redigir um problema realista para o qual esta seja a equação correta. b. Fa