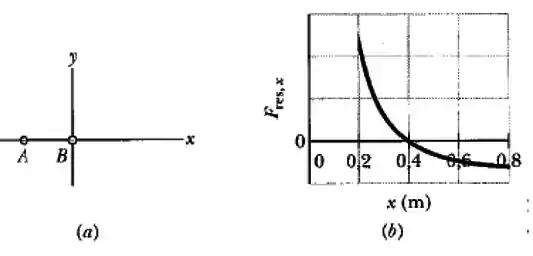
Na figura abaixo, a partícula é mantida fixa em no eixo e a patícula , com uma massa de é mantida na origem. Uma partícula (não mostrada) pode ser deslocada ao longo do eixo , entre a partícula e . A figura mostra o gráfico da força gravitacional resultante exercida pelas partículas e sobre a partícula em função da posição da partícula . O gráfico, na verdade, se estende indefinidamente para a direita tendendo assintoticamente para para . Qual é a massa da partícula e da partícula ?
Considere as massas pontuais e a constante gravitacional .
(a) ,
(b) ,
(c) ,
(d) ,
(e) ,
(f) ,
Passo 1
O gráfico da questão mostra a força sobre a partícula ! Quando a partícula vai pra a única força sobre a partícula é a força exercida pela partícula . O enunciado diz que quando , tende a , assim
Pelo enunciado sabemos que , e . Substituindo temos
Passo 2
Agora pra saber a massa de , podemos olhar qualquer ponto do gráfico. O mais fácil é quando a força resultante é nula!
A força resultante vai ser a soma das forças exercidas por e
Onde tem um sinal de menos na frente por que essa força aponta para esquerda e tem um sinal positivo por que aponta para direita. Assim, como em é nula
Como
Resposta
(b)